java栈和队列的区别 简述栈和队列的区别

文章目录

• 栈和队列
• 栈

• 定义
• 基本概念
• 栈的具体实现
• 顺序栈

• 顺序栈结构体定义：
• 初始化栈
• 空栈判断
• 进栈操作
• 出栈操作
• 获得栈顶元素

• 链栈

• 链栈结构体定义：
• 初始化栈
• 空栈判断
• 进栈操作
• 出栈操作
• 获得栈顶元素

• 栈的应用

• 单词逆序和符号匹配检查
• 递归
• 四则运算表达式求值

• 队列

• 队列的实现
• 顺序队列

• 循环队列
• 顺序队列结构定义：
• 初始化队列
• 求队列长度
• 入队操作
• 出队操作
• 获取队头元素

• 栈式队列

• 栈式队列的结构定义：
• 初始化链式队列
• 链式队列入队操作
• 链式队列出队操作

栈和队列

栈和队列是两种特殊的线性表。 它们的基本操作大致与线性表相同，同时也具有顺序结构和链式结构两种。而其特殊性就体现在两者的不同上。
栈和队列的区别：

• 栈遵循先进后出，队列遵循先进先出。
• 栈只允许表尾进行插入和删除，队列只允许表尾进行插入，表头进行删除。
• 栈常用于实现深度优先遍历，队列常用于实现广度优先遍历。

堆，栈，队列

• 堆，又称为优先队列，遵循队列的原则，但本质是棵二叉树。
• 栈，又称堆栈。
• 队列。

栈的应用

• 递归
• 数值转换
• 四则运算表达式求值
• 括号匹配问题

队列的应用

• 舞伴问题
• 银行排队模拟

栈

定义

栈是限定仅在表尾进行插入和删除操作的线性表，遵循"先进后出（LIFO）"的原则。

栈的开口端被称为栈顶；相应地，封口端被称为栈底。

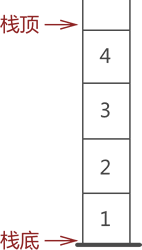
基本概念

进栈和出栈

• 向栈中添加元素，此过程被称为"进栈"（入栈或压栈）；
• 从栈中提取出指定元素，此过程被称为"出栈"（或弹栈）；

栈的具体实现

栈是一种 “特殊” 的线性存储结构，因此栈的具体实现有以下两种方式：

• 顺序栈：采用顺序存储结构实现栈存储结构；
• 链栈：采用链式存储结构实现栈结构；

两种实现方式的区别，仅限于数据元素在实际物理空间上存放的相对位置。

顺序栈

顺序栈结构体定义：

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 
#define MAXSIZE 20 
typedef int SElemType;
typedef int Status; 
typedef struct
{
	SElemType data[MAXSIZE];
    int top; /* 用于栈顶指针 */
}SqStack;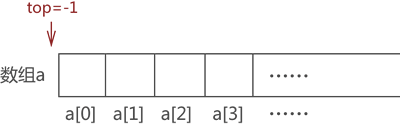

初始化栈

Status InitStack(SqStack *S)
{ 
    S->top = -1;
    return OK;
}

空栈判断

Status StackEmpty(SqStack S)
{ 
    if (S.top == -1)
        return TRUE;
    else
        return FALSE;
}

进栈操作

Status Push(SqStack *S,SElemType e)
{
    /* 栈满 */
    if(S->top == MAXSIZE -1) 
    {
    	return ERROR;
    }
    /* 栈顶指针增加一 */
    S->top++;		
    /* 将新插入元素赋值给栈顶空间 */		
    S->data[S->top] = e;  
    return OK;
}

出栈操作

Status Pop(SqStack *S,SElemType *e)
{ 
    if(S->top == -1)
        return ERROR;
    /* 将要删除的栈顶元素赋值给e */
    *e = S->data[S->top];	
    /* 栈顶指针减一 */
    S->top--;				
    return OK;
}

获得栈顶元素

Status GetTop(SqStack S,SElemType *e)
{
    if (S.top == -1)
        return ERROR;
    else
        *e=S.data[S.top];
    return OK;
}

链栈

以下链栈实现是不含头节点的。

链栈结构体定义：

/* 链栈结构 */
typedef struct StackNode
{
    SElemType data;
    struct StackNode *next;
}StackNode,*LinkStackPtr;

typedef struct
{
    LinkStackPtr top;
    int count;
}LinkStack;

初始化栈

Status InitStack(LinkStack *S)
{ 
    S->top = (LinkStackPtr)malloc(sizeof(StackNode));
    if(!S->top)
        return ERROR;
    S->top = NULL;
    S->count = 0;
    return OK;
}

空栈判断

Status StackEmpty(LinkStack S)
{ 
    if (S.count == 0)
        return TRUE;
    else
        return FALSE;
}

进栈操作

有头插法和尾插法两种，我们采用头插法。

Status Push(LinkStack *S,SElemType e)
{
	LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode)); 
    s->data = e; 
    /* 把当前的栈顶元素赋值给新结点的直接后继*/
    s->next = S->top;	
    /* 将新的结点s赋值给栈顶指*/
    S->top = s;        
    S->count++;
    return OK;
}

出栈操作

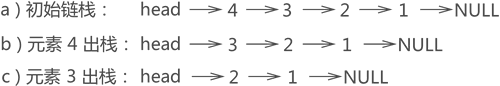
Status Pop(LinkStack *S,SElemType *e)
{ 
    LinkStackPtr p;
    if(StackEmpty(*S))
            return ERROR;
    *e = S->top->data;
    /* 将栈顶结点赋值给p，见图中③ */
    p = S->top;
    /* 使得栈顶指针下移一位，指向后一结点，见图中④ */					
    S->top = S->top->next;    
    /* 释放结点p */
    free(p);                            
    S->count--;
    return OK;
}

获得栈顶元素

Status GetTop(LinkStack S,SElemType *e)
{
    if (S.top == NULL)
        return ERROR;
    else
        *e = S.top->data;
    return OK;
}

栈的应用

单词逆序和符号匹配检查

递归

四则运算表达式求值

队列

定义：队列是只允许在一端进行插入操作，另一端进行删除操作的线性表，遵循 “先进先出” 原则。

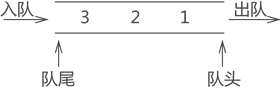
队列的实现

队列存储结构的实现有以下两种方式：

• 顺序队列：在顺序表的基础上实现的队列结构；
• 链队列：在链表的基础上实现的队列结构；

顺序队列

为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素。

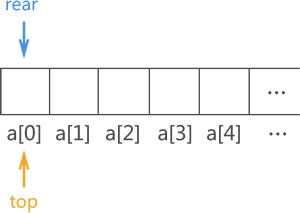
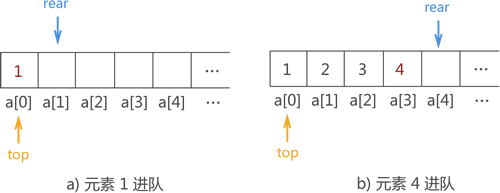
当有数据元素入队时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。

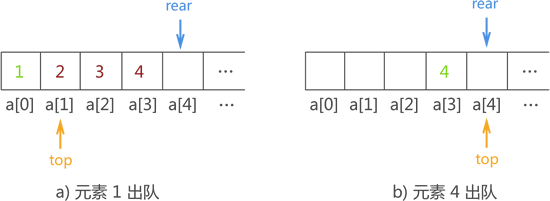
顺序队列整体后移造成的影响是：

• 顺序队列之前的数组存储空间将无法再被使用，造成了空间浪费；
• 如果顺序表申请的空间不足够大，则直接造成程序中数组 a 溢出，产生溢出错误；

所以，就有了顺序队列另一种实现方法：

循环队列

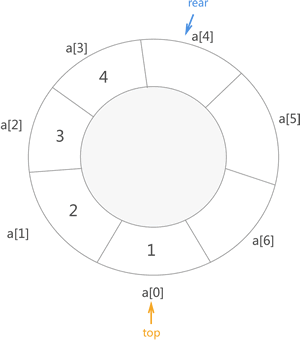
注意：顺序队列的存储状态不同，但是判断条件相同。为了对其进行区分，最简单的解决办法是：牺牲掉数组中的一个存储空间，判断数组满员的条件是：尾指针的下一个位置和头指针相遇，就说明数组满了。

• 队列长度：(rear - front + max)%max
• 队列空的标志：队列的头指针等于队列的尾指针（front == rear）；
• 队列满的判断：队列的头指针等于队列的尾指针（(rear+1)%max==front）

顺序队列结构定义：

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20
typedef struct
{
	QElemType data[MAXSIZE];
	int front;    	/* 头指针 */
	int rear;		/* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}SqQueue;

初始化队列

Status InitQueue(SqQueue *Q)
{
	Q->front=0;
	Q->rear=0;
	return  OK;
}

求队列长度

int QueueLength(SqQueue Q)
{
	return  (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
}

入队操作

Status EnQueue(SqQueue *Q,QElemType e)
{
	if ((Q->rear+1)%MAXSIZE == Q->front)	/* 队列满的判断 */
		return ERROR;
	Q->data[Q->rear]=e;			/* 将元素e赋值给队尾 */
	Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置， */
								/* 若到最后则转到数组头部 */
	return  OK;
}

出队操作

Status DeQueue(SqQueue *Q,QElemType *e)
{
	if (Q->front == Q->rear)			/* 队列空的判断 */
		return ERROR;
	*e=Q->data[Q->front];				/* 将队头元素赋值给e */
	Q->front=(Q->front+1)%MAXSIZE;	/* front指针向后移一位置， */
									/* 若到最后则转到数组头部 */
	return  OK;
}

获取队头元素

Status GetHead(SqQueue Q,QElemType *e)
{
	if(Q.front == Q.rear) /* 队列空 */
		return ERROR;
	*e = Q.data[Q.front];
	return OK;
}

栈式队列

以下代码实现是含有头节点的。

栈式队列的结构定义：

typedef struct QNode	/* 结点结构 */
{
   QElemType data;
   struct QNode *next;
}QNode,*QueuePtr;

typedef struct			/* 队列的链表结构 */
{
   QueuePtr front,rear; /* 队头、队尾指针 */
}LinkQueue;

初始化链式队列

Status InitQueue(LinkQueue *Q)
{ 
	Q->front = Q->rear = (QueuePtr)malloc(sizeof(QNode));
	if(!Q->front)
		exit(OVERFLOW);
	Q->front->next = NULL;
	return OK;
}

链式队列入队操作

链队队列中，当有新的数据元素入队，只需进行以下 3 步操作：

• 将该数据元素用节点包裹，例如新节点名称为 elem；
• 与 rear 指针指向的节点建立逻辑关系，即执行 rear->next = elem；
• 最后移动 rear 指针指向该新节点，即 rear = elem；

Status EnQueue(LinkQueue *Q,QElemType e)
{ 
	QueuePtr s = (QueuePtr)malloc(sizeof(QNode));
	if(!s) /* 存储分配失败 */
		exit(OVERFLOW);
	s->data = e;
	s->next = NULL;
	/* 把拥有元素e的新结点s赋值给原队尾结点的后继*/
	Q->rear->next = s;	
	/* 把当前的s设置为队尾结点，rear指向s */
	Q->rear = s;		
	return OK;
}

链式队列出队操作

链式队列中队头元素出队，需要做以下 3 步操作：

• 通过 front 指针直接找到队头节点，创建一个新指针 p 指向此即将出队的节点；
• 将 p 节点（即要出队的队头节点）从链表中摘除；
• 释放节点 p，回收其所占的内存空间；

Status DeQueue(LinkQueue *Q,QElemType *e)
{
	QueuePtr p;
	if(Q->front == Q->rear)
		return ERROR;
	/* 将欲删除的队头结点暂存给p，见图中① */
	p = Q->front->next;		
	/* 将欲删除的队头结点的值赋值给e */
	*e = p->data;				
	/* 将原队头结点的后继p->next赋值给头结点后继，见图中② */
	Q->front->next = p->next;
	/* 若队头就是队尾，则删除后将rear指向头结点，见图中③ */
	if(Q->rear == p)		
		Q->rear = Q->front;
	free(p);
	return OK;
}