一切从线性回归说起
线性回归的基本形式
对于一个给定的样本,有n个属性对样本进行描述,则该样本可用一下表达式进行描述:
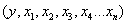
其实x为输入,y为输出。而线性回归的主要任务,就是找出x,y之间的关系,我们可以想象为求解一个线性方程。
在线性模型中,我们就可以将最终结果,看作是所有的输入的线性组合,即如下形式:

这样我们就的得到了线性回归的最基本的模型。为了表达式的简便,我们用同一符号来表示属性,则表达式可做如下形式:

至此我们就得到了线性回归的最基本模型,线性回归的最终结果可以看作是所有输入共同作用下所得到的输出值。
下图既是线性回归的一个图列说明,我们用一条直线,或者一个平面,一个超平面去对样本进行描述,可以看出我们所需的结果是对整体数据集的一个大致描述,而非准确描述。但这种大致的非准确的描述,恰恰是线性回归的精髓与优势,相比于高阶的回归模型,线性回归在计算上的优势更加突出,同时避免了过拟合现象的发生。

线性回归求解
根据上面的例子可以看出,线性回归是在给定输入的情况下对于输出值的预测。仅仅就预测值来看,线性回归已经足够优秀,但是确又不可避免地存在误差。
误差分析:
对于每个样本来说,预测值与实际值之间的关系为:

对于误差所满足的假设条件为:误差是独立同分布的,均值为0,方差为 的高斯分布。举个栗子来说明一下:张三,李四同时去银行贷款,最终贷款多少可能取决于存款,是否有房产,是否有稳定收入等多个因素。此处所说的独立,既张三贷款的多少和李四无关。此处所说的同分布,可以理解为张三李四都在同一家银行贷款。
因为我们的误差函数可写作高斯分布的形式:

带入误差函数有:

于是我们可以构造似然函数:

依据极大似然理论(极大似然理论以及梯度下降法的详细说明见下一博客),此时似然函数的最大值,就是我们所要求的参数 的解。于是我们的任务就转换为似然函数最大值的求解。由于乘积形式计算复杂,求导之后会出现无数项,因为我们把乘积形式换成对数形式,简化计算,构造对数似然函数:

至此,我们已经无线毕竟最终结果,各位看官再坚持一下,马上就会豁然开朗。
观察上式可以看出,最大化似然函数,其实就是最小化
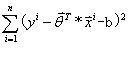
依据以上推导,我们找到了线性回归的损失函数形式,由此我们也就得出了各种博客,西瓜书等等各种公式推导教材中的最小二乘法的最基本形式。其几何意义就是直线或平面外一点到直线或者平面的欧式距离的平方,此处也不难理解,用所有点到直线或平面距离的最小值来对该拟合做评估无疑是一个十分恰当的选择。于是我们的问题变成了 的优化问题。
由于博主懒惰,此处略去该函数为凸函数的证明过程,直接进入凸优化三步走,求导,等于零,得解。

分别令其等于0,于是我们得到了其最优解:

对于参数的求解,我们的常用方法为梯度下降法,所谓梯度下降,简单理解就是沿着函数的梯度方向,每次走一小步,得到新的位置点,再次计算梯度值,再走一小步,不断迭代,通过多次迭代后得到最优解。
例如目标函数为 ,则其梯度下降即为 ,参数的求解为:

其中a称为步长,或学习率。关于梯度下降以及极大似然的更多内容将在以后的博客中给出。





















