上一篇 C语言实现上 中介绍了程序实现时定义的一些数据结构、程序执行的流程以及 程序的基本骨架(详情见 C语言实现上)。留下了两个关键函数computO(i) 和 backUpdate(i) 没有分析实现,参数 i 代表的是第 i 个样本,本篇我们一起来分析下这两个函数的实现。
BP神经网络输出
函数 computO(i) 负责的是通过BP神经网络的机制对样本 i 的输入,预测其输出。回想BP神经网络的基本模型(详情见 基本模型)对应的公式(1)还有 激活函数对应的公式(2):

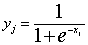
在前篇设计的BP神经网络中,输入层与隐藏层权重对应的数据结构是w[Neuron][In],隐藏层与输出层权重对应的数据结构是v[Out][Neuron],并且数组 o[Neuron] 记录的是神经元通过激活函数对外的输出,BP神经网络预测的样本结果保存在OutputData[Out]中。由此,就可以得到以下实现的参考代码:
void computO(int var){
int i,j;
double sum,y;
/*
神经元输出
*/
for (i = 0; i < Neuron; ++i){
sum=0;
for (j = 0; j < In; ++j)
sum+=w[i][j]*d_in[var][j];
o[i]=1/(1+exp(-1*sum));
}
/* 隐藏层到输出层输出 */
for (i = 0; i < Out; ++i){
sum=0;
for (j = 0; j < Neuron; ++j)
sum+=v[i][j]*o[j];
OutputData[i]=sum;
}
}
BP神经网络的反馈学习
函数 backUpdate(i) 负责的是将预测输出的结果与样本真实的结果进行比对,然后对神经网络中涉及到的权重进行修正,也这是BP神经网络实现的关键所在。如何求到对于 w[Neuron][In] 和 v[Out][Neuron] 进行修正的误差量便是关键所在!误差修正量的求法在基本模型一文中数学分析部分有解答,具体问题具体分析,落实到我们设计的这个BP神经网络上来说,需要得到的是对w[Neuron][In] 和 v[Out][Neuron] 两个数据进行修正误差,误差量用数据结构 dw[Neuron][In] 和 dv[Out][Neuron] 来进行存储。那么来分析下这两个修正误差量是什么样的?推导的思路与基本模型中推导误差量的一致,这里仅列出对具体对于我们设计的BP神经网络中的数学推导过程:

如果你不想知道推导过程,那么只需要看上面中的两个 所以(有三个点的地方) 的内容,就可以知道所需要的误差量是什么样的了;如果想要想弄明白的话,或许需要自己在稿子上画画看推导推导。到这里完成了数学推导,实现的代码就很容易写了。在具体实现对误差修改中,我们再加上学习率,并且对先前学习到的修正误差量进行继承,直白的说就是都乘上一个0到1之间的数,具体的见如下实现参考代码:
#define A 0.2
#define B 0.4
#define a 0.2
#define b 0.3void backUpdate(int var)
{
int i,j;
double t;
for (i = 0; i < Neuron; ++i)
{
t=0;
for (j = 0; j < Out; ++j){
t+=(OutputData[j]-d_out[var][j])*v[j][i];
dv[j][i]=A*dv[j][i]+B*(OutputData[j]-d_out[var][j])*o[i];
v[j][i]-=dv[j][i];
}
for (j = 0; j < In; ++j){
dw[i][j]=a*dw[i][j]+b*t*o[i]*(1-o[i])*d_in[var][j];
w[i][j]-=dw[i][j];
}
}
}
好了,至此BP神经网络的C语言实现就全部完成了。最后,我们可以测试下BP神经网络的运行。我这里是这样给出数据的,两个输入a、b(10以内的数),一个输出 c,c=a+b。换句话说就是教BP神经网络加法运算。在 45个神经元,820个训练样例,样本平均误差小于0.01时完成训练(学习率等见参考代码)的条件下,最后预测 (6,8),(2.1,7),(4.3,8)实际输出结果如下:

最后附上参考实现代码,以及实验训练时的数据、和神经元信息。(本示例 仅为BP神经网络实现的 简单DEMO,若实际使用还需多加考虑!!!)
参考代码下载





















