2022年10月11日 week7

目录
第四讲: RFID高频电路基础
一、RLC(串联)电路的阻抗
二、阻抗计算案例

容抗与感抗的大小随频率变化,即不同的频率,电容、电感所体现的容抗和感抗是不同的。
第四讲: RFID高频电路基础
1.给出下图LRC电路的阻抗表示


一、RLC(串联)电路的阻抗
如果一个电路由R1、R2、R3组成,那么它的电阻很容易计算,下图R=R1+R2+R3;

如果一个电路由R、L、C组成,那么它的阻抗是多少?难道也是电阻和阻抗的累加吗?不是!

我们知道,当电路中有电感、电容器件时,电路不再表现出纯电阻特性,而要用阻抗来描述,阻抗(Impedance)相对于电阻(Resistance)来说。考虑了两方面因素:
1.输入信号的频率对阻抗的影响,2.计算电压U和电流I的相位差异;
纯电感的阻抗称为“感抗”,用符号

表示;纯电容的阻抗称为“容抗”,用符号

表示;
它们统称为“电抗”(Reactance)。
理想情况下,电阻消耗能量;电容、电感不消耗能量,只是转化能量。
因为这种本质上的差异,数学上将电阻与电抗(电容/电感)用正交坐标系的二维坐标来表示,横坐标表示电阻,纵坐标表示电抗,特别的,正半轴表示电感感抗,负半轴表示电容容抗:

上图为阻抗坐标系,复数坐标系下,横坐标电阻为实部,纵坐标电容、电感等电抗为虚部;二维坐标系中,Z(阻抗)可以用复数表示,包含了模|Z|和角度θ两个信息。不过工程上,阻抗常指Z的模——|Z|,上图中已列举了计算公式。
角度θ隐含了电压U和电流I之间的相位信息:
如果为正数,表示电压U在相位上领先于电流I;
如果为负数,表示电流I在相位上领先于电压U。
这方面如果容易搞混,可以从源头去理解,电感的电流不能突变,先变化的是电压,呈现电感特性(XL>XC)的感性电路亦是如此;电容的电压不能突变,先变化的是电流,呈现电容特性(XC>XL)的容性电路亦是如此。
二、阻抗计算案例
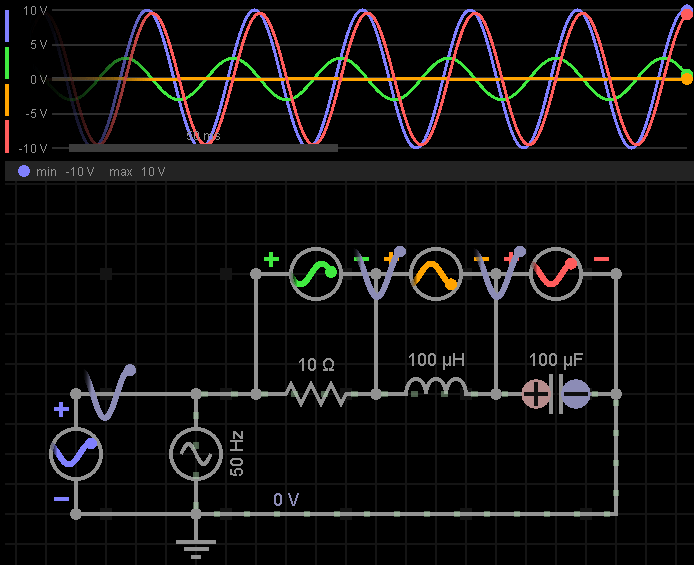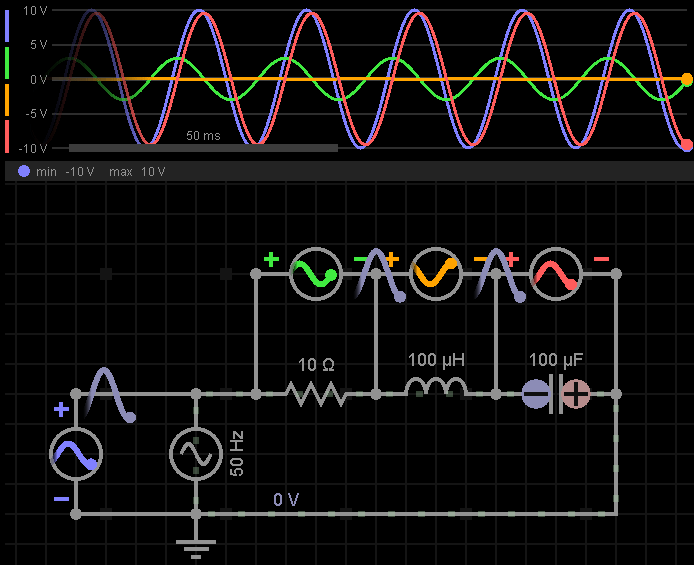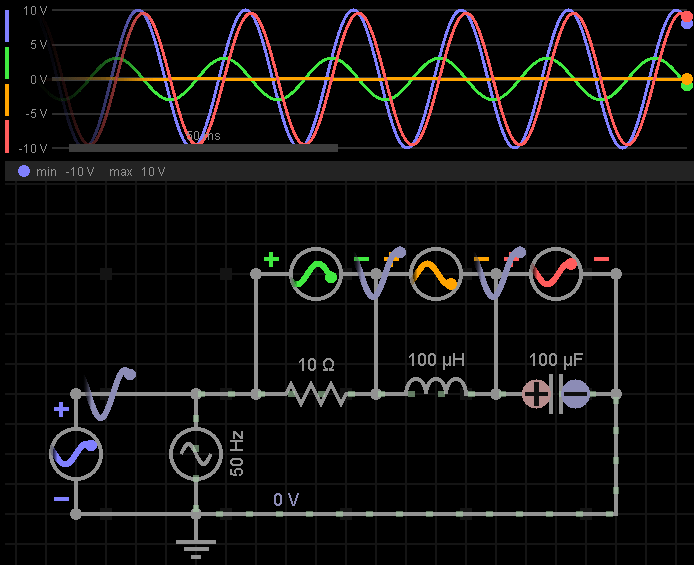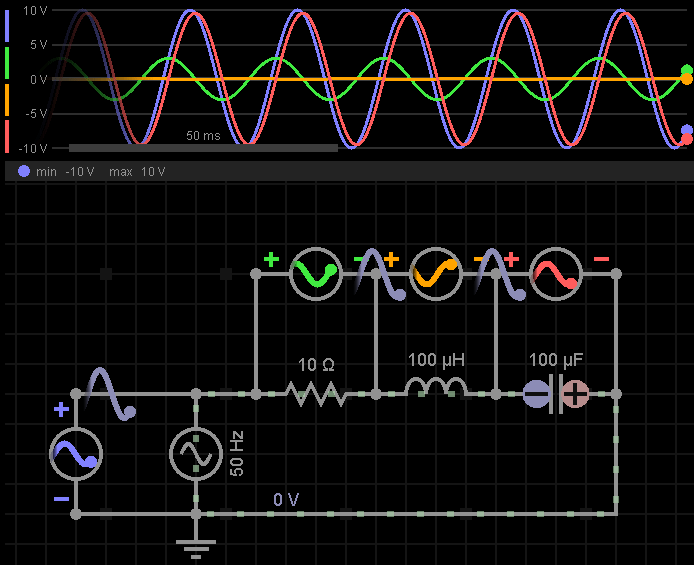
下图中,RLC分别为10Ω、100μH、100μF;输入信号为50Hz,幅度峰值为10V;求电路阻抗、电流有效值?


请注意,通过阻抗算电流或者电压都是基于RMS(有效值)的,所以幅度峰值10V的电源需要乘以0.707算出有效值。
因为是串联电路,所以Irms在所有元器件上一致,我们来分别计算一下电感、电容、电阻上的电压幅度峰值:

可以看到,RLC三者的电压幅度峰值,如果全部加起来是大于电源电压的幅度峰值10V的,之所以这样,因为RLC各自的电压在相位上有差异,在某个具体的时间点(t)上此消彼长,所以加起来不会大于电源电压的幅度峰值10V。
我们来看下仿真波形,体会一下各个元器件上电压的此消彼长:
(2023年 2月18日 09:47首次发布)





















