51 nod 是个好的学习网站，不仅算法分级，而且可以查看别人的优秀代码（过了之后才能查看）。接下来的一些问题就是来自那里。


51 nod 1413 权势二进制（简单数字游戏·贪心）


题目：​​http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1413​​


一个十进制整数被叫做权势二进制，当他的十进制表示的时候只由0或1组成。例如0，1，101，110011都是权势二进制而2，12，900不是。

当给定一个n的时候，计算一下最少要多少个权势二进制相加才能得到n。


Input



单组测试数据。
第一行给出一个整数n (1<=n<=1,000,000)



Output



输出答案占一行。



Input示例



9



Output示例



9


分析：简单的讲，权势二进制就是只由0和1组成的十进制数。有点贪心的意思：比投153=111+11*2+10*2；135=111+11*2+1*2


import java.util.*;
public class Main {
 public static void main(String[] args) {
  Scanner sc=new Scanner(System.in);
  String str;
  int [] m=new int [7];
  while(sc.hasNext()){
   str=sc.next();
   Arrays.fill(m,0);
      int length=str.length();
      for(int i=0;i<length;i++){
       m[i]=str.charAt(i)-48;
      }
      int ans=0;
      for(int i=0;i<length;i++){
       if(m[i]>0){
        ans+=m[i];
           for(int j=i+1;j<length;j++){
            m[j]-=m[i];
           }
       }
      }
      System.out.println(ans);
  }
 }
}


51nod 1381 硬币游戏（简单概率）


​​http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1381​​




有一个简单但是很有趣的游戏。在这个游戏中有一个硬币还有一张桌子，这张桌子上有很多平行线（如下图所示）。两条相邻平行线之间的距离是1，硬币的半径是R，然后我们来抛硬币到桌子上，抛下之后硬币有时候会和一些直线相交（相切的情况也算是相交），有时候不会。

请你来计算一下抛一次硬币之后，该硬币和直线相交数目的期望。



简单问题窥见数学_i++











Input



第一行给出一个整数T，表示有T组数据(1<=T<=10000)。
第2行到T+1，每行给出一个整数R。(0< R <= 10,000,000,000)



Output



对于每一个数据，在一行中输出答案的整数部分即可。



Input示例



1
1



Output示例



2





分析：因为r是一个整数，所以问题好想的多，圆和直线相交的个数有2r+1（相切）和2r两种结果，后者有一个单位长度的线段概率，前者只有一个点的概率。所以答案就是2r.


接下来的一个问题是比赛遇到的：
Rectangle


frog has a piece of paper divided into n rows and m columns. Today, she would like to draw a rectangle whose perimeter is not greater than k.



 


 

简单问题窥见数学_i++_02



 



There are 8(out of 9) ways when n=m=2,k=6
Find the number of ways of drawing.




Input




The input consists of multiple tests. For each test:



 



The first line contains

3


integer

n,m,k


(1≤n,m≤5⋅104,0≤k≤109).





Output




For each test, write

1


integer which denotes the number of ways of drawing.





Sample Input

2 2 6
1 1 0
50000 50000 1000000000

Sample Output

8
0
1562562500625000000
分析：


继续设想：当i=3呢，那么(m-1+1)-->(m-3+1);所以设q=min(n,k/2-1)，j=k/2-i。

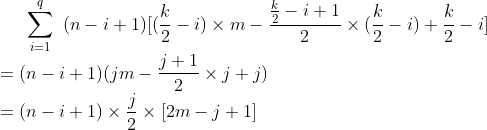
简单问题窥见数学_整除_03



51nod 1393 0和1相等串

​​http://www.51nod.com/onlineJudge/questionCode.html#problemId=1393¬iceId=23885​​




给定一个0-1串，请找到一个尽可能长的子串，其中包含的0与1的个数相等。






Input



一个字符串，只包含01，长度不超过1000000。



Output



一行一个整数，最长的0与1的个数相等的子串的长度。



Input示例



1011



Output示例



2




分析：为了让统计数据变化，将所有的0变成-1，一次遍历。观察规律：

     1  0  0   0  1

0   1  0 -1 -2 -1

计算数据反映了变化的趋势。 寻找sum[i]=sum[j] 长度就是最大的j-i.


#include <iostream> //一定要让计算数据变化
#include <cstdio>
#include <cstring>
#include <map>
using namespace std;
const int maxn=1e6+5;
char str[maxn];
int p[maxn];
int main()
{
    //freopen("cin.txt","r",stdin);
    while(~scanf("%s",str+1)){
        int length=strlen(str+1);
        int ans=0;
        memset(p,0,sizeof(p));
        map<int,int> mp; //默认0
        for(int i=1;i<=length;i++){
            if(str[i]=='1') p[i]=p[i-1]+1;
            else p[i]=p[i-1]-1;
            if(mp[p[i]]==0&&p[i]!=0)mp[p[i]]=i;
            if(i!=1){
                ans=max(ans,i-mp[p[i]]);
                //cout<<i<<" "<<p[i]<<" "<<mp[p[i]]<<endl;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}


学习了别人的代码（来自“姿态决定命运”）：加长数组的宽度，和上面的哈希思想类似。可以看出不用STL确实快了好多。400ms VS 31ms


#define LEN 1000001
int v[LEN*2];
char s[LEN];
int main()
{
    int len,dis=0,ret=0;
    scanf("%s",s);
    len=strlen(s);
    memset(v,-1,sizeof(v));
    for(int i=0;i<len;i++)
    {
        if(s[i]=='1')
            dis++;
        else
            dis--;
        if(v[dis+LEN]==-1&&dis!=0)
        {
            v[dis+LEN]=i;
        }
        else
        {
            if(ret<i-v[dis+LEN])
                ret=i-v[dis+LEN];
        }
    }
    printf("%d\n",ret);
}


51nod 1417 天堂里的游戏（博弈&数学推导）



​​http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1417​​




······

正当Noder惊魂未定的时候，走来一个美女，要求和他一起玩个数学游戏。美女提议：“让我们各自亮出硬币的一面，或正或反。如果我们都是正面，那么我给你A元，如果我们都是反面，我给你B元（A + B为偶数）。剩下的情况你给我（A + B） / 2元就可以了。

Noder知道这个游戏他多半要输，可他并不在乎，他只想让自己输的慢一点。

那么你来帮美女计算一下，她选择出正面的概率应该是多少（以最简分数形式输出）？

当Noder输光了钱后从草地上醒来，吉普赛姑娘已经不见了，只留下了这样一张塔罗牌，上面印有那个美女的照片。

简单问题窥见数学_整除_04

关于样例的解释：

美 女采取了(3/8,5/8)这个方案，不论Noder采用什么方案，都是不能改变局面的。如果全部出正面，每次的期望收益是 (3+3+3-2-2-2-2-2)/8=-1/8元；如果全部出反面，每次的期望收益也是(-2-2-2+1+1+1+1+1)/8=-1/8元。而任 何策略无非只是上面两种策略的线性组合，所以期望还是-1/8元。





Input



第1行：一个数T，表示后面用作输入测试的数的数量（1 <= T <= 20)。
第2 - T + 1行：每行2个数A, B中间用空格分隔。(1 <= A, B <= 10^9，且A + B为偶数)。



Output



输出共T行，对应美女选择正面的概率，以最简分数形式输出，具体请参看输出样例。



Input示例



2
3 1
1 3



Output示例



3/8
5/8




分析：



依据样例分析，全部选定正面和反面的结果应该是一样的，最后一定是女性胜利。那么设女性选择正面的概率是x，正面的A元-->a，反面的B元-->b，
有这样的等式：




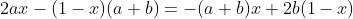
简单问题窥见数学_整除_05



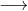
简单问题窥见数学_整除_06



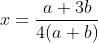
简单问题窥见数学_练习_07




import java.util.*;
public class Main {
    static long gcd(long a,long b){
        return b>0?gcd(b,a%b):a;
    }
    public static void main(String[] args) {
        Scanner sc=new Scanner (System.in);
        long t=sc.nextInt(),a,b;
        for(int k=0;k<t;k++){
            a=sc.nextInt();
            b=sc.nextInt();
            long q1=a+3*b;
            long q2=4*(a+b);
            long r=gcd(q1,q2);
            //System.out.println(q1+" "+q2+" "+r);
            q1=q1/r;
            q2=q2/r;
            System.out.println(q1+"/"+q2);
        }
    }

}


51nod 1433 0和5（整除的规律）




题目：​​http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1433​​​
​






小K手中有n张牌，每张牌上有一个一位数的数，这个字数不是0就是5。小K从这些牌在抽出任意张（不能抽0张），排成一行这样就组成了一个数。使得这个数尽可能大，而且可以被90整除。

注意：

1.这个数没有前导0，

2.小K不需要使用所有的牌。






Input



每个测试数据输入共2行。
第一行给出一个n，表示n张牌。(1<=n<=1000)
第二行给出n个整数a[0],a[1],a[2],…,a[n-1] (a[i]是0或5 ) 表示牌上的数字。



Output



共一行，表示由所给牌组成的可以被90整除的最大的数，如果没有答案则输出”-1”（没有引号）



Input示例



4
5 0 5 0



Output示例



0




分析：2k,3k,5k数字整除和2,3,5有些联系，所有被2整除的数字都是偶数，那么能被2的倍数整除的数字也是偶数，即m%2=0，m是偶数； n%(2k)=0，n也是偶数；m%3=0，m各位上的数字之和是3的倍数，能被9整除的数字各位的数字之和也是9的倍数；能被5整除的数字末尾要么是0要么是5，能被10整数的数字末尾一定是0.


import java.util.*; 
public class Main {
 static int min(int a,int b){  return a<b?a:b; }
 public static void main(String[] args) {
        Scanner sc=new Scanner (System.in);
        int n,a,five,zero;
        while(sc.hasNext()){
         n=sc.nextInt();
         five=0;
         for(int i=0;i<n;i++){
          a=sc.nextInt();
          if(a==5) five++; 
         }
         zero=n-five;
         int k=five/9;
         k=min(k,zero);
         if(k>0){
          for(int i=0;i<k;i++){
                 for(int j=0;j<9;j++) System.out.printf("5");
                }
          //for(int i=0;i<k;i++) 
             for(int i=0;i<zero;i++) System.out.printf("0");
             System.out.println();
         }
         else {
          if(zero==0){  System.out.println(-1); continue; }
          System.out.println(0);
         }
        }
 }
}