那些可以整除的数字

定理1：如果

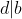
且正整数j<k，

，

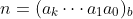
能被

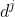
整除，那么

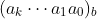
能够被

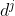
整除 。

比如：

我们知道12564能被2整除，因为

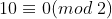
  且4%2=0。进一步，

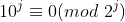
，12564能被4整除，因为64%4=0。而564%8!=0，所以12564%8!=0同样，我们可以解释某些数字为什么能被5整数，能被

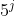
整除

定理2： 如果

，

，

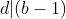
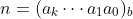
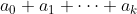
能被d,那么该数字就能被d整除

比如：

我们知道 12312能被3整除，将数字12312展开成10进制后，

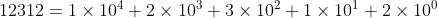
，因为

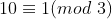
，进一步有

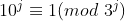
  所以，

 同样，因为

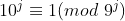
，所以9和3拥有相同的整除性质

定理3：如果

，

，

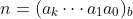
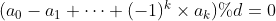
，那么n%d=0。

比如：

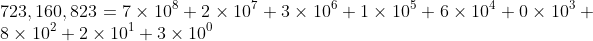
因为

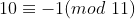
，有：

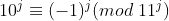
那么，3-2+8-0+6-1+3-2+7=22%11=0，所以该数字能被11整除

由定理3可以得到数字7,11,13的整除判断：

因为

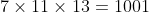
，那么有：

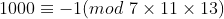
，所以对于一个数字

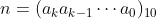
，如果有

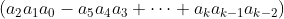
%1001=0，那么该数字能被7,11,13整除。

如果被其中某一个数字整除，那么n能就被该数字整除。

比如：

数字n=59,358,208，208-358+59=-91能被7和13整除，但是不能被11整除，所以n能被7和13整除，但是不能够被11整除

献上一题：

nyist 105 九的余数

​​http://acm.nyist.net/JudgeOnline/problem.php?pid=105​​

现在给你一个自然数n，它的位数小于等于一百万，现在你要做的就是求出这个数整除九之后的余数。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=1e6+10;
char str[N];
int main()
{
    int t;
    cin>>t;
    while(t--){
        scanf("%s",str);
        int len=strlen(str);
        int ans=0;
        for(int i=0;i<len;i++){
            ans=(ans+str[i]-'0')%9;
        }
        printf("%d\n",ans);
    }
    return 0;
}