方法:NORM_MINMAX
输出结果:
输入:[10, 23, 22, 10, 5]
输出:[0.27777779, 1, 0.94444442, 0.27777779, 0]
当前的数组是一行,我们归一化利用的
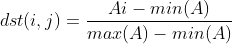
我们来带入进行求解 max(A)=23 ,min(A)=5 所以说:max(A)-min(A)=23-5=17 Ai-min(A)=10-5=5 5/17=0.2777779
那么这个时候我们的输入的矩阵只有一行,如果存在多行,应该怎么来计算
输入:[10, 23, 22, 10, 5;
11, 9, 4, 15, 2]
输出:[0.38095239, 1, 0.95238101, 0.38095239, 0.14285713;
0.42857146, 0.33333334, 0.095238097, 0.61904764, 0]
上面的是还适用吗:
我们来带入进行求解 max(A)=23 ,min(A)=2 所以说:max(A)-min(A)=23-2=21 Ai-min(A)=10-2=8 8/21=0.38095239
看来 NORM_MINMAX 归一化的方式就是矩阵中的每一个元素减去最小的元素然后除以(矩阵中最大的元素减去最小的元素)
方法NORM_L1
输入:
[10, 23, 22, 10, 5;
11, 9, 4, 15, 2]
输出:
[0.090090096, 0.20720722, 0.1981982, 0.090090096, 0.045045048;
0.0990991, 0.081081085, 0.036036037, 0.13513514, 0.018018018]
计算公式:
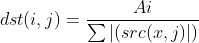
我们按照计算公司来看:矩阵的元素和为:10+23+ 22+10+5+11+9+4+15+2=111 第一个元素:10/111=0.090090096
由此可以看到的是NORM_L1归一化处理是对应元素除以矩阵元素和
方法NORM_L2
查看结果:
输入:[10, 23, 22, 10, 5;
11, 9, 4, 15, 2]
输出:[0.24361277, 0.56030935, 0.5359481, 0.24361277, 0.12180638;
0.26797405, 0.2192515, 0.097445108, 0.36541915, 0.048722554]
计算公式:
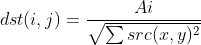
我们来计算一下10*10+23*23+22*22+10*10+5*5+11*11+9*9+4*4+15*15+2*2=1685 求解1685的平方根为:41.048751503547585 然后我们求解第一个元素:10/41.048751503547585 =0.24361276856704797 这个和我们输出元素是一样的
那么我们可以看出NORM_L2 是对应元素除以所有元素的平方和的算术平方根
方法:NORM_INF
查看结果:
输入结果:[10, 23, 22, 10, 5;
11, 9, 4, 15, 2]
输出:[0.43478262, 1, 0.95652175, 0.43478262, 0.21739131;
0.47826087, 0.39130434, 0.17391305, 0.65217394, 0.086956523]
这个计算是比较简单的
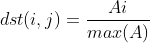
上述的矩阵中最大的元素是23 第一个元素10 所以在输出的时候第一个元素为:10/23=0.43478260869565216
NORM_INF 归一化的方式是对应元素除以矩阵中的最大的元素
总结:
NORM_MINMAX 归一化的方式就是矩阵中的每一个元素减去最小的元素然后除以(矩阵中最大的元素减去最小的元素)对应公式:
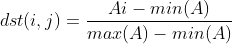
NORM_L1归一化处理是对应元素除以矩阵元素和 对应公式:
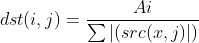
矩阵元素的绝对值之和(曼哈顿距离)NORM_L2 是对应元素除以所有元素的平方和的算术平方根 对应公式:
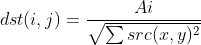
矩阵各元素的欧几里德距离之和NORM_INF 归一化的方式是对应元素除以矩阵中的最大的元素 对应公式:
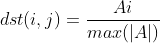
矩阵各元素绝对值的最大值(切比雪夫距离)
上面是对归一化函数有一个初步的了解,以及对应的熟悉公式,看完这些感觉业务了解算法,上学的时候学习的那点知识还真的是需要恶补,特别是学习opencv,当然我们最终的目的不是说对opencv有所创新,我们希望的是对图片可以进行相关的处理,目的地还有很远,继续加油。还有3天要过年了,提前祝大家牛年快乐。
希望对你有所帮助!






















