[HDU5564] Clarke and digits
![f[u+1][(Mod*10+i)\%7 ][i]+=f[u][Mod][pre] 数位DP进阶_#include](https://s2.51cto.com/images/blog/202207/05094755_62c3984ba5e1830470.gif)
发现每一位转移都是一样的, 于是可以矩阵乘法, 把 f[Mod][pre] 压成 Mod * 10 + pre 一个状态
初始状态 ![\rightarrow f[(i \%7)*10+i] = 1 数位DP进阶_#include_02](https://s2.51cto.com/images/blog/202207/05094756_62c3984cd3bf341830.gif)
因为求的是和, 所以还有开一维记录前缀和
发现只有 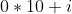 才有贡献, 把这几位设成 1 就可以了
才有贡献, 把这几位设成 1 就可以了
#include<cstdio>
#include<cstring>
#define N 75
using namespace std;
const int Mod = 1000000007;
typedef long long ll;
ll add(ll a, ll b){ return (a+b) % Mod;}
ll mul(ll a, ll b){ return (a*b) % Mod;}
struct Matrix{
ll a[N][N];
Matrix(){ memset(a, 0, sizeof(a));}
friend Matrix operator * (const Matrix &A, const Matrix &B){
Matrix C;
for(int i=0; i<=70; i++)
for(int j=0; j<=70; j++)
for(int k=0; k<=70; k++)
C.a[i][j] = add(C.a[i][j], mul(A.a[i][k], B.a[k][j]));
return C;
}
};
int T, l, r, K;
Matrix power(Matrix a, int b){
Matrix ans; for(int i=0; i<=70; i++) ans.a[i][i] = 1;
for(;b;b>>=1){ if(b&1) ans = ans * a; a = a * a;}
return ans;
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d%d%d", &l, &r, &K);
Matrix A, B, T;
for(int i=0; i<7; i++){
for(int j=0; j<=9; j++){
for(int k=0; k<=9; k++){
if(j + k == K) continue;
int x = i * 10 + j, y = ((i * 10 + k) % 7) * 10 + k;
T.a[x][y] = 1;
}
}
}
for(int i=0; i<=9; i++) T.a[i][70] = 1; T.a[70][70] = 1;
for(int i=1; i<=9; i++) A.a[0][(i % 7) * 10 + i] = 1;
ll ans = 0;
B = A * power(T, l-1);
ans = add(ans, Mod - B.a[0][70]);
B = A * power(T, r);
ans = add(ans, B.a[0][70]);
printf("%lld\n", ans);
} return 0;
}
我们先考虑挪到第1位的代价, 这就是个比较裸的数位DP, f[u][sum] 表示第u位和为sum的答案
然后考虑从1往后挪动, 挪动可以减少的贡献就是中间点右边的和 - 左边和, 再做一遍数位DP
如果减少的贡献小于0, 很明显它不需要挪动了, 赋成0就可以了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll L, R, f[80][1200]; int k, a[80], cnt;
ll dfs1(int u, int sum, bool lim){
if(u == 0) return sum;
if(!lim && f[u][sum] != -1) return f[u][sum];
ll res = 0; int up = lim ? a[u] : (k-1);
for(int i=0; i<=up; i++){
res += dfs1(u-1, sum + i * (cnt - u), lim && (i == up));
} if(!lim) f[u][sum] = res; return res;
}
ll dfs2(int u, int sum, int pos, bool lim){
if(u == 0) return max(sum, 0);
if(!lim && f[u][sum] != -1) return f[u][sum];
ll res = 0; int up = lim ? a[u] : (k-1);
for(int i=0; i<=up; i++){
res += dfs2(u-1, sum + ((u > pos) ? -i : i), pos, lim && (i == up));
} if(!lim) f[u][sum] = res; return res;
}
ll Solve(ll x, int k){
cnt = 0; while(x) a[++cnt] = x % k, x /= k;
memset(f, -1, sizeof(f));
ll ans = dfs1(cnt, 0, 1);
for(int i=cnt-1; i>=1; i--){
memset(f, -1, sizeof(f));
ans -= dfs2(cnt, 0, i, 1);
} return ans;
}
int main(){
scanf("%lld%lld%d", &L, &R, &k);
printf("%lld", Solve(R, k) - Solve(L-1, k));
}
CF908G New Year and Original Order [Hard]
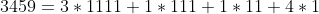
类似套路地考虑, 把贡献拆开, 比如说第一位填3, 我们在填1, 2, 3的时候都记上3的贡献, 对答案是不会影响的
于是我们只需要记录这一位大于等于某个数的方案数
![f[i][j][k][lim] 数位DP进阶_#include_05](https://s2.51cto.com/images/blog/202207/05094759_62c3984f6a15430875.gif) 表示前i位, 有j位 >= k的方案数, 它对答案的贡献就是
表示前i位, 有j位 >= k的方案数, 它对答案的贡献就是  (j 个 1)
(j 个 1)
转移直接暴力枚举, 边界 ![\rightarrow f[0][0][i][lim] = 1 数位DP进阶_#include_07](https://s2.51cto.com/images/blog/202207/05094801_62c39851336d86773.gif)
#include<bits/stdc++.h>
#define N 705
using namespace std;
typedef long long ll;
int n, a[N]; char s[N]; ll f[N][N][10][2];
const int Mod = 1000000007;
ll add(ll &a, ll b){ a = (a+b) % Mod;}
ll mul(ll a, ll b){ return (a*b) % Mod;}
int main(){
scanf("%s", s+1); n = strlen(s+1);
for(int i=1; i<=n; i++) a[i] = s[i] - '0';
for(int i=0; i<=9; i++) f[0][0][i][0] = 1;
for(int i=0; i<n; i++)
for(int j=0; j<=i; j++)
for(int k=1; k<=9; k++)
for(int l=0; l<=1; l++)
for(int p=0; p<=(l?9:a[i+1]); p++)
add(f[i+1][j+(p>=k)][k][l|(p<a[i+1])], f[i][j][k][l]);
ll ans = 0;
for(int k=1; k<=9; k++){
ll tmp = 1;
for(int j=1; j<=n; j++){
add(ans, mul(tmp, (f[n][j][k][0] + f[n][j][k][1]) % Mod));
tmp = mul(tmp, 10); add(tmp, 1);
}
} printf("%lld", ans); return 0;
}





















