【POJ 2154】Color

1.​​题目链接​​。给一个正边形和n中颜色，用这n种颜色给这个正n边形染色，有多少种方案，这里的正n边形是可以旋转的，旋转得到为同一种方案被视为一种。

2.十分裸的Polya问题。

                                                    

Q是置换的个数，lamada(q)是每种置换下，可以被表示为循环的个数。m是m种颜色。直接对应到这个题就是：

                                                                          

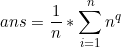
在环上时，每k步轮换得到的循环乘积=gcd(n,k),所以就可以继续写成：

                                                                      

到了这里，就不多说了，套路，直接随便化简一下完事：

                                                                  

（ps:图片是我截acdreamers大神的，因为懒的写latex表达式了，这个东东的化简还是蛮简单的）

然后就直接写代码完事了。

#include <stdio.h>
#include <string.h>
#define N 36000
int n,p;
int pr[N];
bool prime[N];
void init()
{
  int k = 0;
  memset(prime, true, sizeof(prime));
  for (int i = 2; i < N; i++)
  {
    if (prime[i])
    {
      pr[k++] = i;
      for (int j = i + i; j < N; j += i)
      {
        prime[j] = false;
      }
    }
  }
}
int phi(int n)
{
  int rea = n, i;
  for (i = 0; pr[i] * pr[i] <= n; i++)
  {
    if (n % pr[i] == 0)
    {
      rea = rea - rea / pr[i];
      while (n % pr[i] == 0)  n /= pr[i];
    }
  }
  if (n > 1)
    rea = rea - rea / n;
  return rea % p;
}

int qpow(int a, int b)
{
  int ans = 1;
  a %= p;
  while (b)
  {
    if (b & 1)
    {
      ans = ans * a % p;
      b--;
    }
    b >>= 1;
    a = a * a % p;
  }
  return ans;
}

int main()
{
  int  t;
  init();
  scanf("%d", &t);
  while (t--)
  {
    int ans = 0;
    scanf("%d%d", &n, &p);
    for (int i = 1; i * i <= n; i++)
    {
      if (i * i == n)
        ans = (ans + qpow(n, i - 1) * phi(i)%p) % p;
      else if (n % i == 0)
        ans = (ans + qpow(n, i - 1) * phi(n / i)%p + qpow(n, n / i - 1) * phi(i)%p) % p;
    }
    printf("%d\n", ans % p);
  }
  return 0;
}