【HDU 5942】Just a Math Problem

1.题目链接。题目意思十分的明显，明摆着就是推导公式然后求值，实际上是一个很棒的数论题。

2.首先我们可以看出来，f(i)代表能够整除i的素因子的种类。而g(i)=pow(2,f(i)).为什么是2的f(i)次方，这其实是这个题目的突破口，假设该数有k个因子:

                                  

其实就是把这k个素因子分为两个互不相交的集合，也就是k=P*Q[gcd(P,Q)==1]所有的(P,Q)的对数。

那么问题就转换为：

                                                          

然后开始我们的老套路，Mobius反演开始：

                                                        

这个时候，我们枚举d，设P=k*d,Q=t*d.那么就可以继续化简：

                                                        

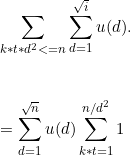
到这里，对于后边的求和式子，枚举一下t(或者k):

                                                   

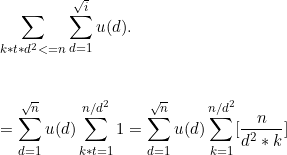
然后整除分块算一下就OK。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1000000 + 5;
const int MOD = 1e9 + 7;
typedef long long ll;
bool check[MAXN + 10];
int prime[MAXN + 10];
int mu[MAXN + 10];
void Moblus()
{
  memset(check, false, sizeof(check));
  mu[1] = 1;
  int tot = 0;
  for (int i = 2; i <= MAXN; i++)
  {
    if (!check[i])
    {
      prime[tot++] = i;
      mu[i] = -1;
    }
    for (int j = 0; j < tot; j++)
    {
      if (i * prime[j] > MAXN)
        break;
      check[i * prime[j]] = true;
      if (i % prime[j] == 0)
      {
        mu[i * prime[j]] = 0;
        break;
      }
      else
      {
        mu[i * prime[j]] = -mu[i];
      }
    }
  }
}

inline ll cal(ll n)
{
  ll ret = 0;
  ll l, r;
  for (l = 1; l * l <= n; l++)
    ret += n / l;
  for (ll t = n / l; l <= n; l = r + 1, t--)
    r = n / t, ret += (r - l + 1) * t % MOD;
  return ret % MOD;
}

inline ll solve(ll n)
{
  ll ret = 0;
  for (int i = 1; (ll)i * i <= n; i++)
  {
    if (mu[i])
    {
      ret += mu[i] == 1 ? cal(n / i / i) : MOD - cal(n / i / i);
      if (ret >= MOD)
        ret -= MOD;
    }
  }
  return (ret + MOD) % MOD;
}

int main()
{
  Moblus();
  int T;
  scanf("%d", &T);
  for (int ca = 1; ca <= T; ca++)
  {
    ll n;
    scanf("%lld", &n);
    printf("Case #%d: %lld\n", ca, solve(n));
  }
  return 0;
}