
一、冒泡排序
原理:
比较两个相邻的元素,将值大的元素交换到右边。
比如:
要排序数组:[10,1,35,61,89,36,55]
第一趟排序:
第一次排序:10和1比较,10大于1,交换位置 [1,10,35,61,89,36,55]
第二次排序:10和35比较,10小于35,不交换位置 [1,10,35,61,89,36,55]
第三次排序:35和61比较,35小于61,不交换位置 [1,10,35,61,89,36,55]
第四次排序:61和89比较,61小于89,不交换位置 [1,10,35,61,89,36,55]
第五次排序:89和36比较,89大于36,交换位置 [1,10,35,61,36,89,55]
第六次排序:89和55比较,89大于55,交换位置 [1,10,35,61,36,55,89]
第一趟总共进行了6次比较,排序结果:[1,10,35,61,36,55,89]
最大的数跑到了最后,下一趟就不用再比较这个数。
第二趟排序:
第一次排序:1和10比较,1小于10,不交换位置 1,10,35,61,36,55,89
第二次排序:10和35比较,10小于35,不交换位置 1,10,35,61,36,55,89
第三次排序:35和61比较,35小于61,不交换位置 1,10,35,61,36,55,89
第四次排序:61和36比较,61大于36,交换位置 1,10,35,36,61,55,89
第五次排序:61和55比较,61大于55,交换位置 1,10,35,36,55,61,89
第二趟总共进行了5次比较,排序结果:1,10,35,36,55,61,89
第三趟排序:
第一次排序:1和10比较,1小于10,不交换位置 1,10,35,36,55,61,89
第二次排序:10和35比较,10小于35,不交换位置 1,10,35,36,55,61,89
第三次排序:35和36比较,35小于36,不交换位置 1,10,35,36,55,61,89
第四次排序:36和61比较,36小于61,不交换位置 1,10,35,36,55,61,89
第三趟总共进行了4次比较,排序结果:1,10,35,36,55,61,89
分析:N个数字要排序,总共进行N-1趟排序,每i趟的排序次数为(N-i)次。
代码实现:
/**
* 冒泡排序
* @Author Feng, Ge
*/
public static void bubbleSort(long[] arr){
long start = System.currentTimeMillis();
if(arr==null || arr.length < 2 ){
return;
}
for(int i=0; i<arr.length-1; i++){
System.out.println("第" + (i+1)+"趟");
for (int j=0; j<arr.length-i-1; j++){
if(arr[j] > arr[j+1]){
long temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
long end = System.currentTimeMillis();
System.out.println("冒泡排序耗时:" + (end-start));
}
public static void main(String[] args){
long[] arr = {81,57,34,32,6,91,19,25,36,34};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print("、");
}
System.out.println("");
bubbleSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print("、");
}
System.out.println("");
}
排序前:
81、57、34、32、6、91、19、25、36、34、
第1趟
第2趟
第3趟
第4趟
第5趟
第6趟
第7趟
第8趟
第9趟
冒泡排序耗时:1
排序后:
6、19、25、32、34、34、36、57、81、91、
上面的是最原始的冒泡排序,总共9趟才完成排序,下面是冒泡的改进版:
public static void bubbleSort(long[] arr) {
long start = System.currentTimeMillis();
if (arr == null || arr.length < 2) {
return;
}
boolean flag = true;
for (int i = 0; i < arr.length - 1; i++) {
flag = true;
System.out.println("第" + (i+1)+"趟");
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
long temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false;
}
}
if(flag){
break;
}
}
long end = System.currentTimeMillis();
System.out.println("冒泡排序耗时:" + (end - start));
}
排序前:
81、57、34、32、6、91、19、25、36、34、
第1趟
第2趟
第3趟
第4趟
第5趟
第6趟
冒泡排序耗时:0
排序后:
6、19、25、32、34、34、36、57、81、91、
增加flag可以使得原本就有序的趟不用在执行,能有效减少不必要的比较,这里改进后只执行了6趟。
时间复杂度:
冒泡排序总的平均时间复杂度为:O(n2) ,时间复杂度和数据状况无关。
二、快速排序
快速排序是冒泡排序的改进版,比冒泡算法快很多(为啥快这么多,一会讲讲完原理和代码就会明白)。
原理:
快速排序首先在这个序列中随便找一个数作为基准,然后把小于这个基准的数放在基准的左边,大于基准的放在右边,然后分别在左右两边选择新的基准,重复上面的过程(对应代码里面的递归)。
比如:{5,7,6,1,9,10,4,2,3,8}这个数组
先在这个数组选择一个数作为基准,一般选择第一个,就选5作为基准。
采用双向指针的形式,定义分别指向数组的最开始和最尾端的位置:
首先将j向左移,直到j指向的数小于5;
再将i向右移,直到i指向的数大于5。最终i指向7,j指向3。
将3和7交换,数组变为{5,3,2,1,9,10,4,6,7,8}。第一次交换结束。
接下来继续探测、交换,探测、交换…
第二次交换结束后数组变为{5,3,2,1,4,10,9,6,7,8}。
j指向9的位置,i指向4的位置,j继续向左移动,直到i的位置才找到小于5的值。
此时i=j,我们只需将基准数落在这个位置:将5和4的值交换。数组变为{4,3,2,1,5,10,9,6,7,8}。

至此,第一轮交换结束。
数组被划分为两个区,基准数5左边是小于5的{4,3,2,1},基准右边是大于5的{10,9,6,7,8}。
再分别对这两个区进行第二轮交换。整个过程如下:
再比如上面冒泡排序中的数组,快速排序过程如下(圈起来的为所选的基准数):
代码实现:
public static void quickSort(long[] arr,int low,int high){
int i,j;
long temp;
long t;
if(low>high){
return;
}
i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i<j) {
//先看右边,依次往左递减
while (temp<=arr[j]&&i<j) {
j--;
}
//再看左边,依次往右递增
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
public static long[] createArray(int len, int max) {
long[] arr = new long[len];
for (int i = 0; i < arr.length; i++) {
arr[i] = (long) (Math.random() * max);
}
return arr;
}
public static void main(String[] args){
long []arr=createArray(10, 100);
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print("、");
}
System.out.println("");
quickSort(arr,0, arr.length-1);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print("、");
}
System.out.println("");
}
排序前:
8、24、3、80、11、72、30、65、71、43、
排序后:
3、8、11、24、30、43、65、71、72、80、
时间复杂度:
快速排序最优的情况下时间复杂度为:O( nlogn );
快速排序的平均时间复杂度也是:O(nlogn);
快速排序最差的情况下时间复杂度为:O( n^2 )
三、选择排序
原理:
先找到数组中最小的元素,然后将它和数组的第一个元素交换位置(如果这个元素其实就是自己本身的话,那么就和自己本身进行交换)。然后在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置,以此循环下去,整个排序过程只需要遍历 n-1 趟。
代码实现:
public class SelectSortDemo {
public static long[] createArray(int len, int max) {
long[] arr = new long[len];
for (int i = 0; i < arr.length; i++) {
arr[i] = (long) (Math.random() * max);
}
return arr;
}
public static void main(String[] args) {
long[] arr = createArray(10, 100);
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print("、");
}
System.out.println("");
selectSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print("、");
}
System.out.println("");
}
public static long[] selectSort(long[] data) {
if (data.length == 0 || data.length == 1) {
return data;
}
for (int i = 0; i < data.length - 1; i++) {
// 假设最开始时,i位置的数最小
int min = i;
for (int j = i + 1; j < data.length; j++) {
if (data[min] > data[j]) {
// 此时最小的位置移动到j,最小的数即data[j]
min = j;
}
}
// 调换min位置和i位置的值(若一轮比较下来都没有变更最小值的索引,即min==i,则无需调换顺序)
if (min != i) {
long temp = data[min];
data[min] = data[i];
data[i] = temp;
}
}
return data;
}
}
排序前:
70、77、52、24、81、45、69、78、45、69、
排序后:
24、45、45、52、69、69、70、77、78、81、
时间复杂度:
java选择排序算法是一种不稳定的算法,它的时间复杂度为 O(n2),空间复杂度为 O(1)。
四、插入排序
就像打扑克牌,假如你先拿到牌1,5,9 然后你又起了一个8这时候你需要和1,5,9比较然后把8插入到5,9的中间让它成为有序的1,5,8,9 。详细看下面动图。
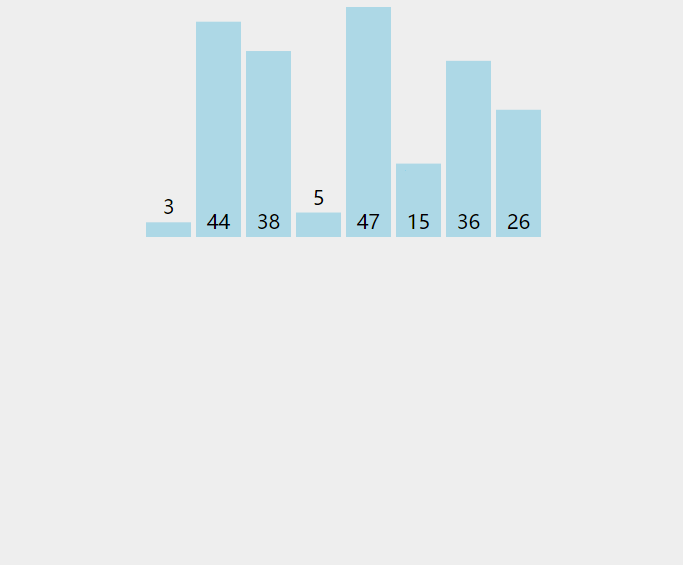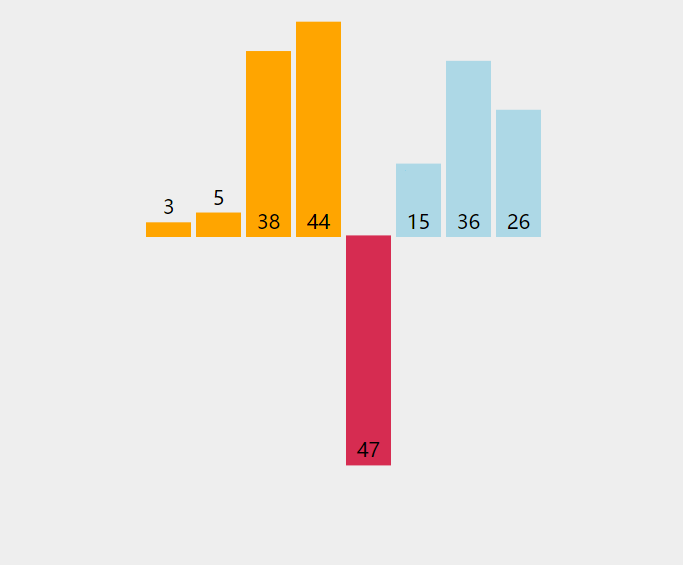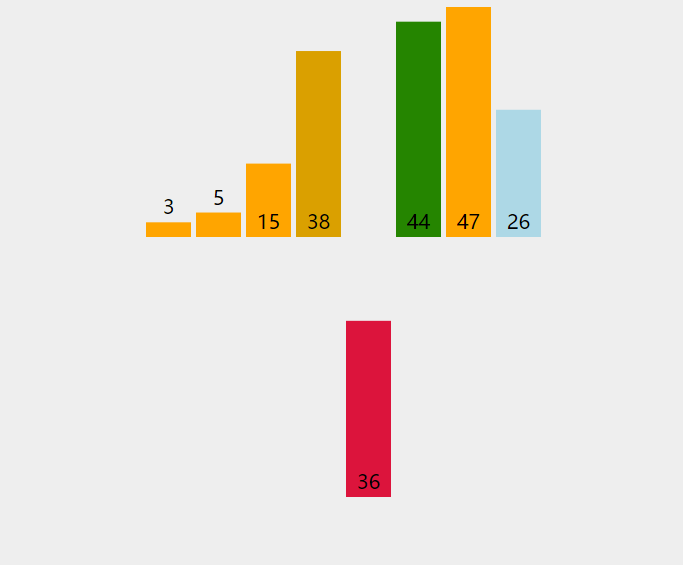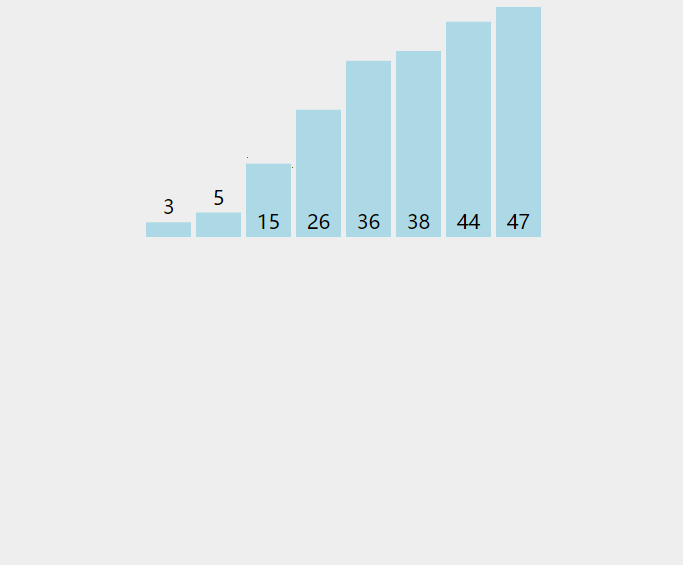
插入排序是一种简单且稳定的算法,适用于已排好序的序列,往其他插入某个元素,保证数据有序。
它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个形成一个有序表。
代码实现:
public class InsertionSort {
public static void main(String[] args) {
int[] arr = {3, 44, 38, 5, 47, 15, 36, 26};
insertionSort(arr);
Console.log(arr);
}
private static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j-1]>arr[j]) {
int temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
}
}
}
}
[3, 5, 15, 26, 36, 38, 44, 47]
时间复杂度:
空间复杂度O(1) 时间复杂度外层循环n次 内层循环(1+2+3+…+i+…+n)所以复杂度是n的平放 最优的时间复杂度O(n)。
五、希尔排序
希尔排序是插入排序的一种更高效的改进版本,是基于插入排序的特性的优化。
插入排序的特性是:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
希尔排序的基本思想是:
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
在大多数元素已经有序的情况下,插入排序的工作量较小;在元素数量较少的情况下,插入排序的工作量较小。
所谓分组,就是让元素两两一组,同组两个元素之间的跨度,都是数组总长度的一半,也就是跨度为4 = 8/2。
如图所示,元素(5,9)一组,元素(8, 2)一组,元素(6, 1)一组,元素(3,7)一组,一共4组。
接下来,我们让每组元素进行独立排序,排序方式用直接插入排序即可。由于每一组的元素数量很少,只有两个,所以插入排序的工作量很少。每组排序完成后的数组如下:
这样一来,仅仅经过几次简单的交换,数组整体的有序程度得到了显著提高,使得后续再进行直接插入排序的工作量大大减少。这种做法,可以理解为对原始数组的“粗略调整”。
但是这样还不算完,我们可以进一步缩小分组跨度,重复上述工作。把跨度缩小为原先的一半,也就是跨度为2 = 4/2,重新对元素进行分组:
如图所示,元素(5,1,9,6)一组,元素(2,3,8,7)一组,一共两组。
接下来,我们继续让每组元素进行独立排序,排序方式用直接插入排序即可。每组排序完成后的数组如下:
此时,数组的有序程度进一步提高。
最后,我们把分组跨度进一步减小,让跨度为1=2/1,也就等同于做直接插入排序。经过之前的一系列粗略调整,直接插入排序的工作量减少了很多,排序结果如下:
整个流程:
像这样逐步分组进行粗调,再进行直接插入排序的思想,就是希尔排序。
上面示例中所使用的分组跨度(4,2,1),被称为希尔排序的增量。
代码实现:
public class ShellSort {
public static void main(String[] args) {
int[] arr = {3, 44, 38, 5, 47, 15, 36, 26};
shellSort(arr);
Console.log(arr);
}
public static void shellSort(int[] array) {
// 第一层循环控制间隔
for (int step = array.length / 2; step > 0; step = step / 2) {
// 第二层循环控制同一间隔内各子数组的排序
for (int i = step; i < array.length; i++) {
// j是一个子数组进行插入排序时的游标
int j = i;
int temp = array[j];
// 第三次循环为子数组的插入排序
while (j - step >= 0 && array[j] < array[j - step]) {
array[j] = array[j - step];
j = j - step;
}
array[j] = temp;
}
}
}
}
[3, 5, 15, 36, 26, 38, 44, 47]
时间复杂度:
最好时间复杂度:O(n)
最坏时间复杂度:O(n4/3)~O(n2)
平均时间复杂度:取决于步长
空间复杂度:O(1)
六、基数排序
原理:
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。


基数排序是对传统桶排序的扩展,速度很快。
基数排序是经典的空间换时间的方式,占用内存很大, 当对海量数据排序时,容易造成 OutOfMemoryError 。
代码实现:
public class BasicSort {
public static void main(String[] args) {
int[] arr = {53, 3, 542, 748, 14, 214};
basicSort(arr);
Console.log(arr);
}
public static void basicSort(int a[]) {
int max = 0;
for (int i = 0; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
}
Console.log("数组中最大值:{}", max);
int times = 0;
while (max > 0) {
max = max / 10;
times++;
}
Console.log("需要排序的轮数:{}", times);
// 准备10个桶, 每个桶也是一个ArrayList, 能存储多个数字
List<ArrayList> queen = new ArrayList<>();
for (int i = 0; i < 10; i++) {
ArrayList q = new ArrayList();
queen.add(q);
}
for (int i = 0; i < times; i++) {
Console.log("第{}轮", i);
for (int j = 0; j < a.length; j++) {
int x = a[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
Console.log("a[j]:{}", a[j]);
Console.log("返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):{}", (int) Math.pow(10, i + 1));
Console.log("a[j] % (int) Math.pow(10, i + 1)", a[j] % (int) Math.pow(10, i + 1));
Console.log("(int) Math.pow(10, i)", (int) Math.pow(10, i));
Console.log("x:{}", x);
Console.log("===============================================");
ArrayList q = queen.get(x);
q.add(a[j]);
}
Console.log("queen:{}", queen);
// 循环queen以及它的每个ArrayList元素
int count = 0;
for (int z = 0; z < 10; z++) {
while (queen.get(z).size() > 0) {
ArrayList<Integer> c = queen.get(z);
Console.log("c:{}", c);
a[count] = c.get(0);
Console.log("a[{}]:{}", count, a[count]);
c.remove(0); //一方面是为了一直在get(0)处取值,一方面是为了清空queen
count++;
}
}
}
}
}```
```bash
数组中最大值:748
需要排序的轮数:3
第0轮
a[j]:53
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):10
a[j] % (int) Math.pow(10, i + 1) 3
(int) Math.pow(10, i) 1
x:3
===============================================
a[j]:3
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):10
a[j] % (int) Math.pow(10, i + 1) 3
(int) Math.pow(10, i) 1
x:3
===============================================
a[j]:542
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):10
a[j] % (int) Math.pow(10, i + 1) 2
(int) Math.pow(10, i) 1
x:2
===============================================
a[j]:748
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):10
a[j] % (int) Math.pow(10, i + 1) 8
(int) Math.pow(10, i) 1
x:8
===============================================
a[j]:14
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):10
a[j] % (int) Math.pow(10, i + 1) 4
(int) Math.pow(10, i) 1
x:4
===============================================
a[j]:214
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):10
a[j] % (int) Math.pow(10, i + 1) 4
(int) Math.pow(10, i) 1
x:4
===============================================
queen:[[], [], [542], [53, 3], [14, 214], [], [], [], [748], []]
c:[542]
a[0]:542
c:[53, 3]
a[1]:53
c:[3]
a[2]:3
c:[14, 214]
a[3]:14
c:[214]
a[4]:214
c:[748]
a[5]:748
第1轮
a[j]:542
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):100
a[j] % (int) Math.pow(10, i + 1) 42
(int) Math.pow(10, i) 10
x:4
===============================================
a[j]:53
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):100
a[j] % (int) Math.pow(10, i + 1) 53
(int) Math.pow(10, i) 10
x:5
===============================================
a[j]:3
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):100
a[j] % (int) Math.pow(10, i + 1) 3
(int) Math.pow(10, i) 10
x:0
===============================================
a[j]:14
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):100
a[j] % (int) Math.pow(10, i + 1) 14
(int) Math.pow(10, i) 10
x:1
===============================================
a[j]:214
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):100
a[j] % (int) Math.pow(10, i + 1) 14
(int) Math.pow(10, i) 10
x:1
===============================================
a[j]:748
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):100
a[j] % (int) Math.pow(10, i + 1) 48
(int) Math.pow(10, i) 10
x:4
===============================================
queen:[[3], [14, 214], [], [], [542, 748], [53], [], [], [], []]
c:[3]
a[0]:3
c:[14, 214]
a[1]:14
c:[214]
a[2]:214
c:[542, 748]
a[3]:542
c:[748]
a[4]:748
c:[53]
a[5]:53
第2轮
a[j]:3
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):1000
a[j] % (int) Math.pow(10, i + 1) 3
(int) Math.pow(10, i) 100
x:0
===============================================
a[j]:14
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):1000
a[j] % (int) Math.pow(10, i + 1) 14
(int) Math.pow(10, i) 100
x:0
===============================================
a[j]:214
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):1000
a[j] % (int) Math.pow(10, i + 1) 214
(int) Math.pow(10, i) 100
x:2
===============================================
a[j]:542
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):1000
a[j] % (int) Math.pow(10, i + 1) 542
(int) Math.pow(10, i) 100
x:5
===============================================
a[j]:748
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):1000
a[j] % (int) Math.pow(10, i + 1) 748
(int) Math.pow(10, i) 100
x:7
===============================================
a[j]:53
返回第一个参数的第二个参数次方 (int) Math.pow(10, i + 1):1000
a[j] % (int) Math.pow(10, i + 1) 53
(int) Math.pow(10, i) 100
x:0
===============================================
queen:[[3, 14, 53], [], [214], [], [], [542], [], [748], [], []]
c:[3, 14, 53]
a[0]:3
c:[14, 53]
a[1]:14
c:[53]
a[2]:53
c:[214]
a[3]:214
c:[542]
a[4]:542
c:[748]
a[5]:748
[3, 14, 53, 214, 542, 748]
时间复杂度:
O(n*k) k: “桶”的个数
七、归并排序
原理:
不断的将大的数组分成两个小数组,直到不能拆分为止,即形成了单个值。此时使用合并的排序思想对已经有序的数组进行合并,合并为一个大的数据,不断重复此过程,直到最终所有数据合并到一个数组为止。
在归并之前,首先先要对两个数组做排序,要保证他们两个有序,然后在进行归并。之前的有序的过程可以使用快速排序算法。
在归并中,一般会使用 快排 + 归并 来完成一个数组的排序。

再举个例子:

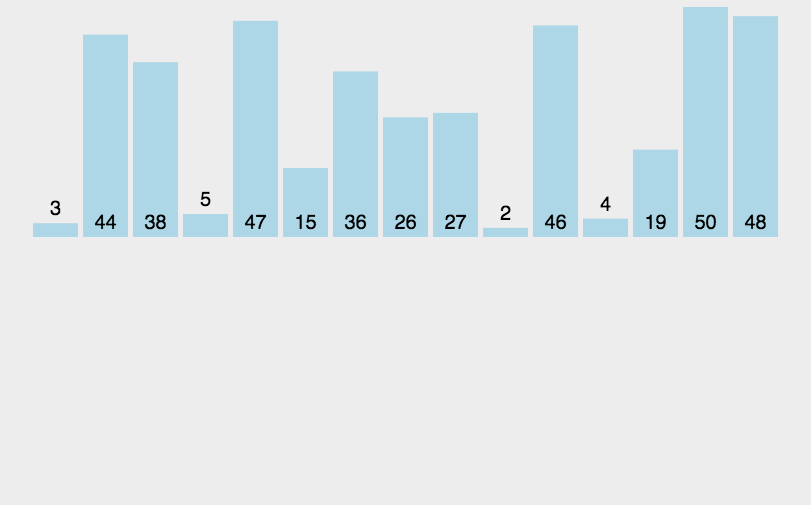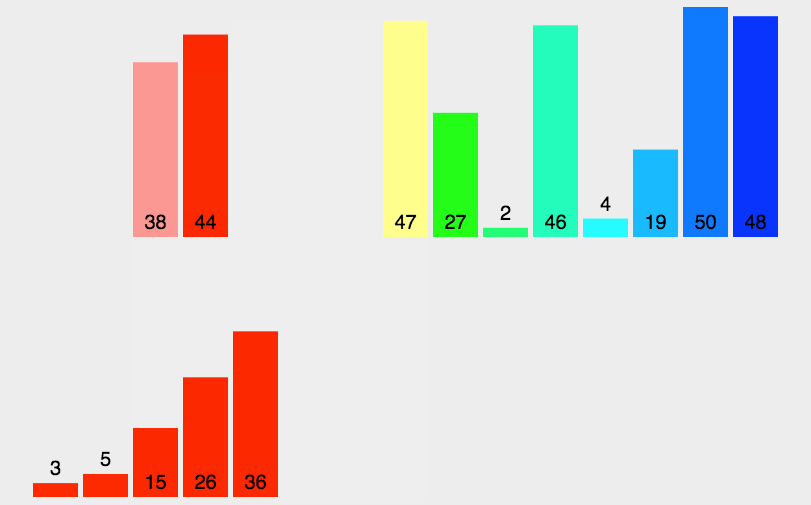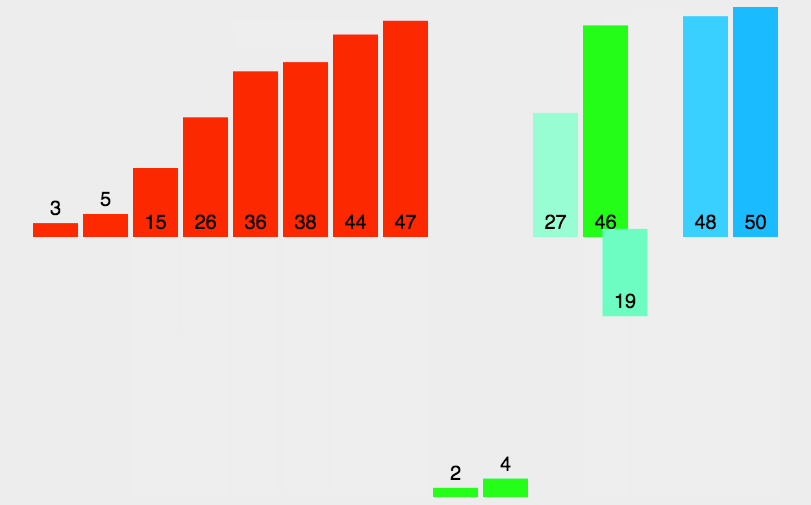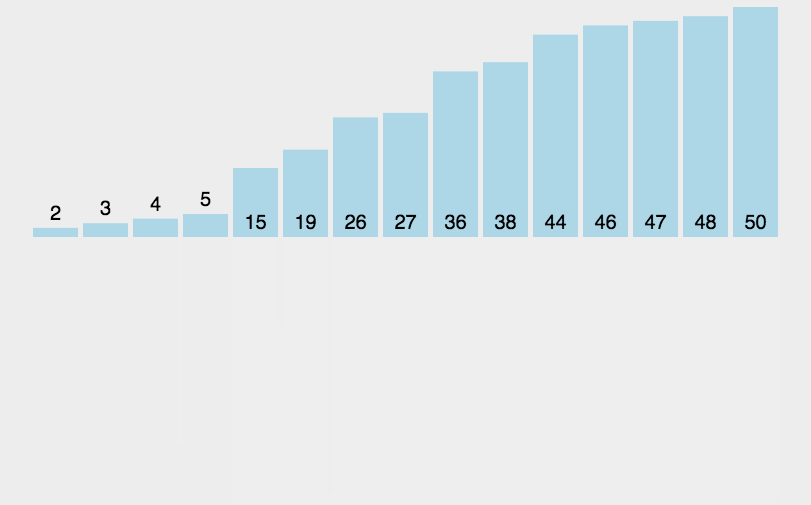
代码实现:
public class MergeSort {
public static void main(String[] args) {
int[] arr = {53, 3, 542, 748, 14, 214};
mergeSort(arr, 0, 5);
Console.log(arr);
}
public static void mergeSort(int[] arr, int low, int high) {
int mid = (low + high) / 2;
if (low < high) {
mergeSort(arr, low, mid);
mergeSort(arr, mid + 1, high);
merge(arr, low, mid, high);
}
}
public static void merge(int a[], int low, int mid, int high) {
int[] temp = new int[high - low + 1];
int i = low;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= high) {
if (a[i] < a[j]) {
temp[k++] = a[i++];
} else {
temp[k++] = a[j++];
}
}
while (i <= mid) {
temp[k++] = a[i++];
}
while (j <= high) {
temp[k++] = a[j++];
}
for (int x = 0; x < temp.length; x++) {
a[x + low] = temp[x];
}
}
}
[3, 14, 53, 214, 542, 748]
时间复杂度:
O(nlogn)
八、堆排序
原理:
预备知识:堆结构

堆是具有以下性质的完全二叉树:
- 每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
- 或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
即子结点的键值总是小于(或者大于)它的父节点。
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中
用于降序排列;
算法步骤:
- 创建一个堆 H[0……n-1];
- 把堆首(最大值)和堆尾互换;
- 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
- 重复步骤 2,直到堆的尺寸为 1。

代码实现:
public class HeapSort {
public static void main(String[] args) {
int[] arr = {53, 3, 542, 748, 14, 214};
heapSort(arr);
Console.log(arr);
}
public static void heapSort(int arr[]) {
int len = arr.length;
for (int i = len / 2 - 1; i >= 0; i--) {
adjustment(arr, i, len);
}
for (int i = len - 1; i >= 0; i--) {
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
adjustment(arr, 0, i);
}
}
public static void adjustment(int arr[], int pos, int len) {
int child = 2 * pos + 1;
if (child + 1 < len && arr[child] > arr[child + 1]) {
child++;
}
if (child < len && arr[pos] > arr[child]) {
int tmp = arr[pos];
arr[pos] = arr[child];
arr[child] = tmp;
adjustment(arr, child, len);
}
}
}[3, 14, 53, 214, 542, 748]
时间复杂度:
堆排序的平均时间复杂度为 Ο(nlogn)。
九、计数排序
原理:
以[1 7 8 7 9 8 10 4]这个序列为例说明计数排序算法的实现原理。
① 未开始排序时
② 先找到待排序序列中最大值10和最小值1
③ 新建一个长度为N=最大值10-最小值1+1=10的数组,新数组中值中值均为0
④ 开始遍历待排序的序列,第一个元素为1,故将值为1的元素放到新数组位置为1的地方,其值为元素1在原序列中出现的次数1次
⑤ 继续遍历,第二个元素为7,故将值为7的元素放到新数组位置为7的地方,其值为元素7在原序列中出现的次数1次
⑥ 继续遍历,第三个元素为8,故将值为8的元素放到新数组位置为8的地方,其值为元素8在原序列中出现的次数1次
⑦ 继续遍历,第四个元素为7,故将值为7的元素放到新数组位置为7的地方,其值为元素7在原序列中出现的次数第2次
⑧ 继续遍历,第五个元素为9,故将值为9的元素放到新数组位置为9的地方,其值为元素9在原序列中出现的次数1次
⑨ 继续遍历,第六个元素为8,故将值为8的元素放到新数组位置为8的地方,其值为元素8在原序列中出现的次数第2次
⑩ 继续遍历,第七个元素为10,故将值为10的元素放到新数组位置为10的地方,其值为元素10在原序列中出现的次数1次
⑪ 继续遍历,第八个元素为4,故将值为4的元素放到新数组位置为4的地方,其值为元素4在原序列中出现的次数1次
⑫ 至此,整个待排序数组遍历完毕,新数组中的每一个值,代表了其下标在待排序数组中出现的次数
⑬ 最后遍历新数组,输出新数组元素的下标值,对应下标的值是几就输出几次
计数排序算法是一个非基于比较的排序算法,故在排序的过程中不存在元素之间的比较和交换操作。计数排序算法是一种以空间换取时间的做法,所以在一定范围内的整数排序时,它是快于任何比较排序算法
优点:速度快
缺点:
- 需要提前知道待排序元素最大值
- 需要大量内存消耗
代码实现:
public class CountSort {
public static void main(String[] args) {
int[] array = {53, 3, 542, 748, 14, 214};
countSort(array);
Console.log(array);
}
protected static void countSort(int[] array) {
//找出最大值和最小值
int max = array[0];
int min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i]>max) {
max= array[i];
}
if (array[i]<min) {
min= array[i];
}
}// O(n)
// 开辟内存空间,存储次数
int[] counts = new int[max-min+1];
// 统计每个整数出现的次数
for (int i = 0; i < array.length; i++) {
counts[array[i]-min]++;
}// O(n)
// 累加次数
for (int i = 1; i < counts.length; i++) {
counts[i]+= counts[i-1];
}
//从后向前遍历元素,将她放在有序数组中的合适位置
int[] newArray = new int[array.length];
for (int i = array.length-1; i >=0 ; i--) {
//获取元素在counts中的索引
int index = array[i]-min;
//获取元素在counts中的值
//counts[index];
//放在合适位置
newArray[--counts[index]] = array[i];
}
// 将有序数组赋值到array
for (int i = 0; i < newArray.length; i++) {
array[i] = newArray[i];
}
}
}
[3, 14, 53, 214, 542, 748]
时间复杂度:
计数排序的空间复杂度为n+O(k)。其中n为待排序元素个数,k为待排序元素最大值
十、桶排序
原理:
将待排序数据分配到有限数量的桶里。每个桶再单独进行子排序,最后按顺序将多个桶中的数据进行合并,排序完成。
桶排序分为4个步骤:
- 划分合适数量的桶。
- 将所有待排序数据放入到对应的桶中。
- 使用合理的算法对每个非空桶进行子排序。
- 按顺序将每个桶中数据进行合并。
① 划分合适数量的桶
根据不同规模和不同范围的数据,我们采取不同的划分方式。目前数据都是0到1之间小数,数据比较均匀,我们等分成4个桶,每个桶的范围都是0.25,效果如下:
② 将所有待排序数据放入到对应的桶中
遍历待排序数据,将每个数据放入对应范围的桶中
③ 使用合理的算法对每个非空桶进行子排序
待排序数据划分到不同桶中后,每个桶中的数据还是无序的
可以看到,第二个桶不用排序,其他桶需要进行排序,分别对每个桶中的数据再使用合适的排序算法,比如快速排序。排序后效果如下图:
④ 按顺序将每个桶中数据进行合并
现在范围小的桶在前面,范围大的桶在后面,并且每个桶中的数据也是从小到大排序的,因此我们只需要从左往右将每个桶中的数据取出放到数组中即可。取出第一个桶后的数据如下:
取出第二个桶后的数据如下:
取出第三个桶后的数据如下:
取出第四个桶后的数据如下:
当所有桶中的数据都取出后排序就完成了。
代码实现:
public class BucketSort {
public static void main(String[] args) {
double[] array = {53, 3, 542, 748, 14, 214};
bucketSort(array);
Console.log(array);
}
public static void bucketSort(double[] arr) {
// 获取最大值和最小值
double max = arr[0];
double min = arr[0];
for (int i = 1; i < arr.length; i++) {
double num = arr[i];
if (num > max)
max =num;
else if (num < min)
min = num;
}
// 桶的数量
int bucketNumber = 4;
// 每个桶的范围
double range = (max - min) / bucketNumber;
// 1.初始化所有桶,每个桶都是LinkedList,方便增加数据
LinkedList<Double>[] buckets = new LinkedList[bucketNumber];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new LinkedList<>();
}
// 2.将所有待排序数据放入到对应的桶中
for (int i = 0; i < arr.length; i++) {
double num = arr[i];
int index = (int) ((num -min)/range);
if(index==bucketNumber)
index-=1;// 如果这个数字正好是最大值,计算出索引就是number,会数组越界,放到最后一个桶中
buckets[index].add(num);
}
// 3.使用合理的算法对每个非空桶进行子排序
for(int i=0;i<buckets.length;i++) {
// 对每个桶中的数据进行排序
Collections.sort(buckets[i]);
}
// 4.按顺序将每个桶中数据进行合并
int index =0;
for(int i=0;i<buckets.length;i++){
LinkedList<Double> bucket=buckets[i];
for(int j =0;j< bucket.size();j++){
arr[index]=bucket.get(j);
index++;
}
}
}
}
[3.0, 14.0, 53.0, 214.0, 542.0, 748.0]
时间复杂度:
当待排序的数组内的数值是均匀分配的时候,桶排序的时间复杂度为O(n)。
十一、位排序
原理:
BitMap的核心思想就是用一个bit位来记录0和1两种状态,将具体数据映射到比特数组的具体某一位上,这个bit位设置为0表示该数不存在,设置为1表示该数存在。由于BitMap使用bit来记录数据,所以大大节省了存储空间,比如上面5亿个数据,如果使用bit来记录,只需要(1.875 / 32)G不到60兆内存即可。
利用这个特性,BitMap很适合用来进行大量数据的排序、去重、查找,包括在线活跃用户的统计,用户签到等。
假如现在有一个待排序的数据: int[] a = {4,7,2,5,3};
取值范围 <8,那么我们初始化8个bit位的数组,并把他们初始化为零:
每一个bit位的取值是0,或者1。 然后把每一个的待排序的数字取出来,根据数字的大小把bit数组的对应下标的bit置为1。
最后会变成这样:
然后,我们从第0未bit开始打印非0位的下标,也就是:23457,也就排好序了。
BitMap是使用内存来进行排序的。
优点:
(1)运算效率高。
(2)占用内存少
缺点:
(1)对重复数据无法进行排序。
(2)数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题,那就可以考虑用 Bloom Filter 来解决,Bloom Filter 使用多个 Hash 函数来减少冲突的概率。
(3)数据稀疏时浪费空间。比如上面举的例子,存入(1, 100000),只有两个数,但我们不得不开足够大的空间来存放100000,这就造成了中间很多空间的浪费,可以通过引入 Roaring BitMap 来解决。
位图排序是一种效率极高并且很节省空间的一种排序方法,但是这种排序方法对输入的数据是有比较严格的要求(数据不能重复,大致知道数据的范围)。
代码实现:
public class BitSet {
private int[] bits;
private final static int ADDRESS_BITS_PER_WORD = 5;
private final static int BITS_PER_WORD = 1 << ADDRESS_BITS_PER_WORD;
/**
* 无参构造器
* 默认构造容量为32bit的数组,即数组长度为1
*/
public BitSet() {
bits = new int[(BITS_PER_WORD - 1) >> ADDRESS_BITS_PER_WORD + 1];
}
/**
* 有参构造器
* @param nbits 数字的个数
*/
public BitSet(int nbits) {
bits = new int[(nbits - 1) >> ADDRESS_BITS_PER_WORD + 1];
}
public int[] getBits() {
return bits;
}
/**
* 把num映射到bits数组中
* @param num
*/
public void set(int num) {
// num在数组中的下标
int index = num >> ADDRESS_BITS_PER_WORD;
// TODO:要检查数组是否需要扩容
bits[index] |= 1 << (num & 0x1F);
}
/**
* 判断bits数组中对应位的值
* @param bitIndex
* @return
*/
public boolean get(int bitIndex) throws Exception {
if (bitIndex < 0) {
throw new Exception();
}
// 把输入的下标进行转换,对应数组某个值的某个位置
int index = bitIndex >> ADDRESS_BITS_PER_WORD;
return (bitIndex < bits.length) && ((bits[index] & (1 << (bitIndex & 0x1F))) != 0);
}
public static void main(String[] args) throws Exception {
// 5亿个数
BitSet bitSet = new BitSet(1_0000_0000);
// 目标数组
int[] arr = {2, 98, 76, 56, 100, 762, 16, 95};
Arrays.stream(arr).forEach(num -> {
bitSet.set(num);
});
// 判断某个数在数组中是否存在
System.out.println(bitSet.get(100)); // true
System.out.println(bitSet.get(200)); // false
System.out.println(bitSet.get(762)); // true
// 输出排序后的数组
int[] res = bitSet.getBits();
int count = 0;
for (int i = 0; i < res.length; i++) {
// 按位输出
for (int j = 0; j < 32; j++) {
// 为1表示该数存在
if (((res[i] >> j) & 1) == 1) {
arr[count++] = i * 32 + j;
}
}
}
// 2 16 56 76 95 98 100 762
Arrays.stream(arr).forEach(System.out::println);
}
}
true
false
true
2
16
56
76
95
98
100
762
****加粗样式时间复杂度:
O(n)























