一、为什么要进行数据归一化
- 定义:把所有数据的特征都归到 [0,1] 之间 或 均值0方差1 的过程。
- 原则:样本的所有特征,在特征空间中,对样本的距离产生的影响是同级的;
- 问题:特征数字化后,由于取值大小不同,造成特征空间中样本点的距离会被个别特征值所主导,而受其它特征的影响比较小;
- 例:特征1 = [1, 3, 2, 6, 5, 7, 9],特征2 = [1000, 3000, 5000, 2000, 4000, 8000, 3000],计算两个样本在特征空间的距离时,主要被特征2所决定;
- 定义:将所有的数据(具体操作时,对每一组特征数据进行分别处理)映射到同一个尺度中;
- 归一化的过程,是算法的一部分;
二、数据归一化的方法
1.最值归一化(MinMaxScaler,normalization)
将特征缩放至特定区间,将特征缩放到给定的最小值和最大值之间,或者也可以将每个特征的最大绝对值转换至单位大小。这种方法是对原始数据的线性变换,将数据归一到[0,1]中间。
转换函数为 : 
其中x为数据集中每一种特征的值,将数据集中的每一种特征都做映射,
特点:
1.多适用于分布有明显边界的情况;如考试成绩、人的身高、颜色的分布等,都有范围;而不是些没有范围约定,或者范围非常大的数据。
2.这种方法对于outlier非常敏感,因为outlier影响了max或min值,且被考虑在计算中了。
3.这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
2. Z-score(StandardScaler,0均值归一化)
标准化数据通过减去均值然后除以方差(或标准差),这种数据标准化方法经过处理后数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
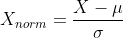
其中
μ:每组特征的均值;σ:每组特征值的标准差;X:每一个特征值;Xnorm:归一化后的特征值;
特点:
1. 适用于 数据的分布本身就服从正态分布的情况。
2. 通常这种方法基本可用于有outlier的情况,但是,在计算方差和均值的时候outliers仍然会影响计算。所以,在出现outliers的情况下可能会出现转换后的数的不同feature分布完全不同的情况。
3. 使用于数据分布没有明显的边界(有可能存在极端的数据值)。
4. 归一化后,数据集中的每一种特征的均值为0,方差为1。
5. 相对于最值归一化的优点是:即使原数据集中有极端值,归一化后,依然满足均值为0方差为1,不会形成一个有偏的数据。
6. 在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,这种方法(Z-score standardization)表现更好。
3. RobustScaler
如果你的数据包含许多异常值,使用均值和方差缩放可能并不是一个很好的选择。这种情况下,你可以使用 robust_scale 以及 RobustScaler 作为替代品。它们对你的数据的中心和范围使用更有鲁棒性的估计。
This Scaler removes the median(中位数) and scales the data according to the quantile range(四分位距离,也就是说排除了outliers)
三、其他细节及说明
1.归一化范围选择[0, 1] 还是 [-1, 1] ?
([-1,1]指存在负数,但是不一定所有数据都在这个范围内,例如下面的实战的截图)
假设我们有一个只有一个hidden layer的多层感知机(MLP)的分类问题。每个hidden unit表示一个超平面,每个超平面是一个分类边界。参数w(weight)决定超平面的方向,参数b(bias)决定超平面离原点的距离。如果b是一些小的随机参数(事实上,b确实被初始化为很小的随机参数),那么所有的超平面都几乎穿过原点。所以,如果data没有中心化在原点周围,那么这个超平面可能没有穿过这些data,也就是说,这些data都在超平面的一侧。这样的话,局部极小点(local minima)很有可能出现。 所以,在这种情况下,标准化到[-1, 1]比[0, 1]更好。
1、在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,StandardScaler表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用MinMaxScaler。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
原因是使用MinMaxScaler,其协方差产生了倍数值的缩放,因此这种方式无法消除量纲对方差、协方差的影响,对PCA分析影响巨大;同时,由于量纲的存在,使用不同的量纲、距离的计算结果会不同。
而在StandardScaler中,新的数据由于对方差进行了归一化,这时候每个维度的量纲其实已经等价了,每个维度都服从均值为0、方差1的正态分布,在计算距离的时候,每个维度都是去量纲化的,避免了不同量纲的选取对距离计算产生的巨大影响。
2. 关于测试数据集的处理
1)问题
- 训练数据集归一化很好理解,用于训练模型,那对于测试数据集如何归一化?
2)方案
- 不能直接对测试数据集按公式进行归一化,而是要使用训练数据集的均值和方差对测试数据集归一化;
3)原因
- 原因1:真实的环境中,数据会源源不断输出进模型,无法求取均值和方差的;
- 原因2:训练数据集是模拟真实环境中的数据,不能直接使用自身的均值和方差;
- 原因3:真实环境中,无法对单个数据进行归一化;
对数据的归一化也是算法的一部分;
4)方式
- (X_test - mean_train) / std_train
- X_test:测试集;
- mean_train:训练集的均值;
- std_train:训练集的标准差;
四、实战代码解析
1.自己实现前两种归一化:
import numpy as np
x = np.random.randint(0, 100, size = 100) # 范围[0,100)注意左闭右开
x = np.array(x, dtype=float)
x = (x - np.min(x)) / (np.max(x) - np.min(x)) # 这样的操作是合法的
xx = np.random.randint(0, 100, size = (50,2) )
xx = xx.astype('float32')
xx[:,0] = (xx[:,0]-np.mean(xx[:,0]))/np.std(xx[:,0])
xx[:,1] = (xx[:,1]-np.mean(xx[:,1]))/np.std(xx[:,1])
得到:


可以发现,最值归一化时,操作后的数据中一定会有0和1,且都是非负数。
0均值归一化时,数据有正有负,且不一定在[-1,1]范围内。
2.学习使用scikit-learn中的Scaler类
假设numpy数据的行数为数据样本个数,列数为特征数。
方法1:使用 sklearn.preprocessing.scale
>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
>>> X_scaled = preprocessing.scale(X_train)
>>> X_scaled
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
sklearn.preprocessing.scale可以沿着特定的坐标轴对数据集进行归一化,在均值附近集中化数据并缩放至单位方差.
参数包括:sklearn.preprocessing.scale(X, axis = 0, with_mean=True, with_std=True, copy=True)
X:需要进行集中化和缩放的数据,类似于数组,稀疏矩阵
axis:整数(默认是 0 )用来计算均值和标准差的轴. 当 axis=0 时,对各个特征进行标准化;当 axis=1 时,会对每个样本进行标准化
with_mean:boolean,布尔型,默认是 True,即在缩放之前对数据进行集中化
with_std:boolean,布尔型,默认是 True,即缩放数据至单位方差( 或单位标准差)
copy:boolean,布尔型,默认是 True,可选填. 设置为 False 的时候即在原数据行上进行标准化,并禁止复制( 如果输入是 numpy 数组或是 scipy.sparse CSC 矩阵并且 axis = 1)
方法2:使用 sklearn.preprocessing.StandardScaler
- scikit-learn中将训练数据集的均值和方差封装在了类Scalar中;

其中:fit:根据训练数据集获取均值和方差,scikit-learn中返回一个Scalar对象;
transform:对训练数据集、测试数据集进行归一化;
- 实例化StandardScaler()时,不需要传入参数;
- 归一化并没有改变数据集,而是又生成一个新的矩阵,一般不要改变原数据;
实战代码的具体步骤:
数据分割——导入并实例化归一化模块——fit(得到均值和方差)——transform(得到归一化后的数据集) ——继续后续操作
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 1)归一化前,将原始数据分割
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.2,
stratify=y, # 按照标签来分层采样
shuffle=True, # 是否先打乱数据的顺序再划分
random_state=1) # 控制将样本随机打乱
# 2)导入均值方差归一化模块:StandardScaler
from sklearn.preprocessing import StandardScaler
# 实例化,不需要传入参数
standardScaler = StandardScaler()
# 3)fit过程:返回StandardScaler对象,对象内包含训练数据集的均值和方差
# fit过程,传入训练数据集;
standardScaler.fit(X_train)
# 输出:StandardScaler(copy=True, with_mean=True, with_std=True)
# fit后可通过standardScaler查看均值和标准差
# standardScaler.mean_:查看均值
# standardScaler.scale_:查看标准差
# 4)transform:对训练数据集和测试数据集进行归一化,分别传入对应的数据集
# 归一化并没有改变训练数据集,而是又生成一个新的矩阵,除非将新生成的数据集赋给原数据集,一般不改变原数据
X_train_standard = standardScaler.transform(X_train)
np.mean(X_train_standard[:,0])
np.var(X_train_standard[:,0])
X_test_standard = standardScaler.transform(X_test)
# 接下来就是使用归一化后的数据集训练并测试模型
4. scikit-learn的StandardScaler类中的内部逻辑
import numpy as np
class StandardScaler:
def __init__(self):
self.mean_ = None
self.scale_ = None
def fit(self, X):
"""根据训练数据集获取均值和标准差"""
assert X.ndim == 2,"the dimension of X must be 2"
self.mean_ = np.array([np.mean(X[:,i]) for i in range(0,X.shape[1])])
self.scale_ = np.array([np.std(X[:,i]) for i in range(0,X.shape[1])])
return self
def transform(self, X):
"""将X根据这个StandardScaler进行均值方差归一化处理"""
assert X_train.ndim == 2, "the dimension of X_train must be 2"
assert self.mean_ is not None and self.scale_ is not None,\
"must fit before transform"
assert X.shape[1] == len(self.mean_),\
"the feature number of X must be equal to mean_ and std_"
reasX = np.empty(shape=X.shape, dtype=float)
for col in range(X.shape[1]):
resX[:,col] = (X[:,col] - self.mean_[col]) / self.scale_[col]
return resX





















