快速选择算法简介

快速选择算法解决的问题指的是，有一个n个数的序列，求出这个序列从小到大排序后的第k小数。一般情况下我们遇到这种题，优先会想到先把序列排序后，直接输出第k小的数，排序的复杂度一般为$O(nlogn)$，因此一般来说只能做$10^5$，如果数据规模再大，这样的复杂度就无法胜任要求。这时候我们就需要使用快速选择算法，快速选择算法可以在时间复杂度为$0(n)$的情况下求出第k小数。

快速选择算法流程

快速选择算法是基于快速排序的过程的，因此，算法是在快排基础上进行操作的。（快排见以前博客）

  1. 找分界点
  2. 调整区间
  3. 递归排序左区间，递归排序右区间 快速选择算法是在执行完第二步，在递归处理的时候实现的，如下图 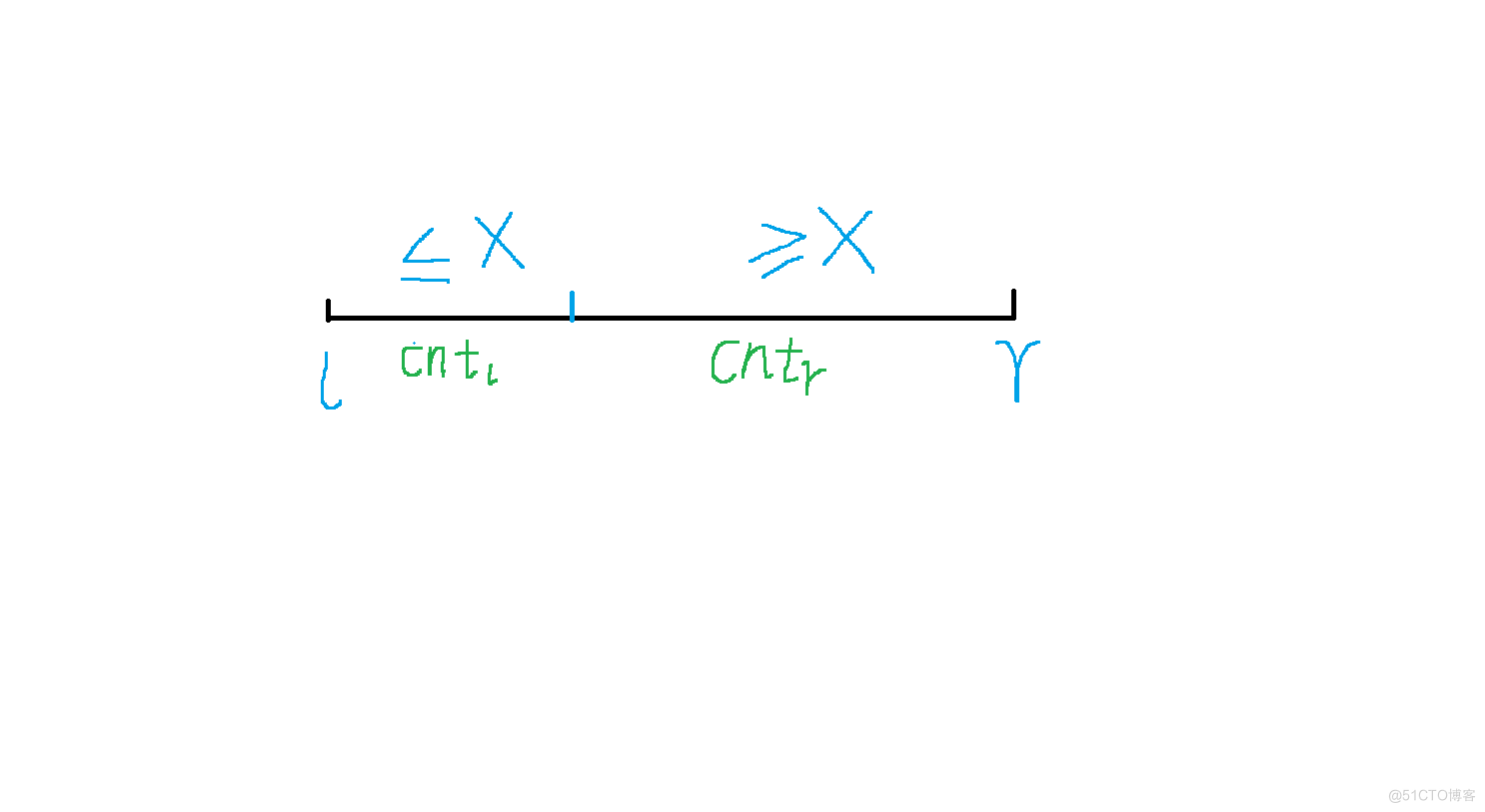快速选择.png 调整完区间后，我们不妨设左半边区间里元素个数为$cntl$，右半边区间里元素个数为$cntr$，因为左半边元素一定小于右半边元素，因此，我们只需要判断$k$与$cntl$谁大，如果$k<=cntl$，则说明区间的第k小数一定在左半边，此时我们只需要递归左半边即可，否则，如果$k>cntl$，则证明第k小数不在左边，而是在右半边，此时我们只需要递归右半边寻找即可。但是，我们需要注意的是，如果是递归左半边，递归的实际上是左半边的第$k$小数，但是如果递归的是右半边，则下一次递归相当于是在右半边区间内找右半段区间的第$k-cntl$小数。

快速选择算法模板

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n;
int q[N];
int quick_sort(int l, int r, int k)
{
    if (l == r)
        return q[l];
    int i = l - 1, j = r + 1, x = q[l + r >>1];
    while (i < j)
    {
        do (i ++); while(q[i] < x);
        do (j --); while(q[j] > x);
        if (i < j)
            swap(q[i], q[j]);
    }
    int sl = j - l + 1;
    if (sl >= k)
        return quick_sort(l, j, k);
    else
        return quick_sort(j + 1, r, k - sl);
        
}
int main()
{
    int k;
    cin >> n >> k;
    for (int i = 0; i < n; i ++)
        cin >> q[i];
    cout << quick_sort(0, n-1, k);
    return 0;
}

代码解释 1.代码第二十行，是为了求出左半边有多少个元素，上述循环结束后，j指针到了i指针前边，左半边的元素就是$l$到$j$之间的所有元素 2.代码第而是一行之后就是判断第k小元素到底是在那半边，如果是左边，就是左边第k小的元素，如果是右边就是第$k-sl$小的元素。

笔记参考

Acwing算法基础课