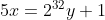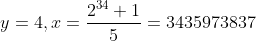魔鬼数字_

进公司之前对于魔鬼数字的理解，是真魔鬼。

进公司之后发现，2也是魔鬼数字。

收录一下真魔鬼的魔鬼数字。

1，开方的近似计算 0x1fbd1df5

float MagicSqrt(float x)
{
  float xhalf = x / 2;
  int i = *(int*)&x;
  i = 0x1fbd1df5 + (i >> 1);
  return *(float*)&i;
}

int main()
{
  cout << MagicSqrt(2);
  return 0;
}

输出1.47748

如果再加牛顿法进行精度优化：

float MagicSqrt(float x)
{
  float xhalf = x / 2;
  int i = *(int*)&x;
  i = 0x1fbd1df5 + (i >> 1);
  x = *(float*)&i;
  x = x / 2 + xhalf / x;
  x = x / 2 + xhalf / x;
  return x;
}

int main()
{
  cout << MagicSqrt(2);
  return 0;
}

输出1.41421

输入5000输出70.7107，误差不到0.0001

2，开方原理

​

3，开方倒数的近似计算

float rsqrt(float number)
{
  float y = number;
  long i = *(long *)&y;
  i = 0x5f3759df - (i >> 1);
  y = *(float *)&i;
  return y;
}

int main()
{
  cout << rsqrt(2);
  return 0;
}

输出0.716215

4，开方倒数原理

5，除法换成乘法 3435973837

求一个5的倍数除5等于多少，可以换成乘法

int main()
{
  cout << 100*3435973837;
  return 0;
}

输出20

原理很简单：

cout << 3435973837 * 5;  会输出1，发生了溢出截断。

那么这个数是怎么来的呢？也很简单，解不定方程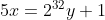

最小解是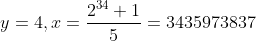

除了5之外，其他所有奇数几乎都可以这么搞。