本文是 2020人工神经网络第一次作业 的参考答案第七部分
➤07 第七题参考答案
1.题目分析
使用AutoEncoder对于下面样本进行压缩:

▲ 样本英文字符
说明:上面数据可以从作业文件:ABCDEFJ.TXT中获得对应的编码数据。
A = [0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]
B = [1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
C = [0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
D = [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
E = [1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
F = [1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
G = [0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
H = [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]
I = [0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
J = [0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
2.网络构成
构造AutoEncoder神经网络,其中隐层的节点数量从2 变化到20。隐层神经元传递函数为sigmoid函数,网络的输出为线性函数。

▲ 神经网络结构
上述网络的Python实现请参见后面附件中::作业1-7中的程序
3.网络训练
使用所有样本训练网络,学习速率:。
下图显示了隐层节点从1个到10个之间网络误差随着训练步骤增加下降的情况。
可以看到隐层节点阅读,网络误差下降越快。
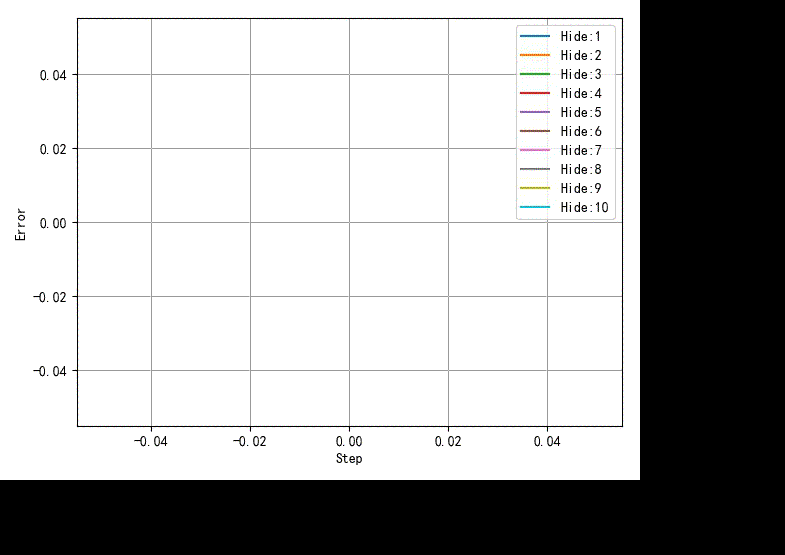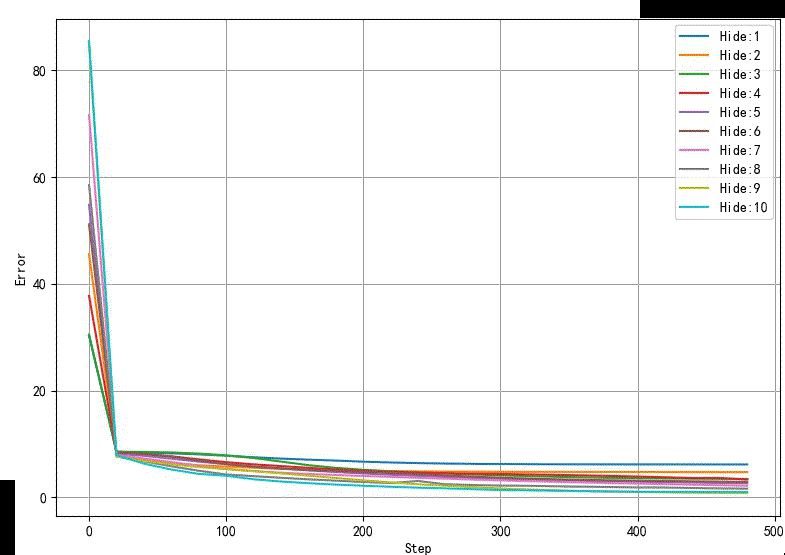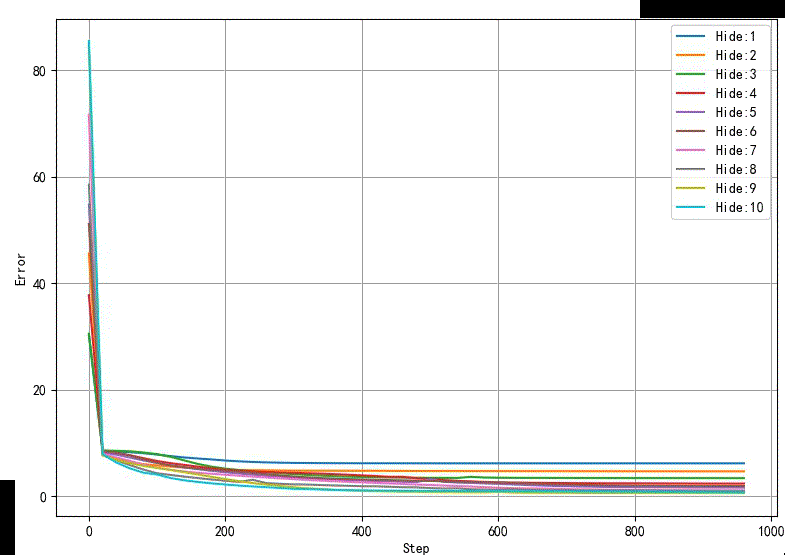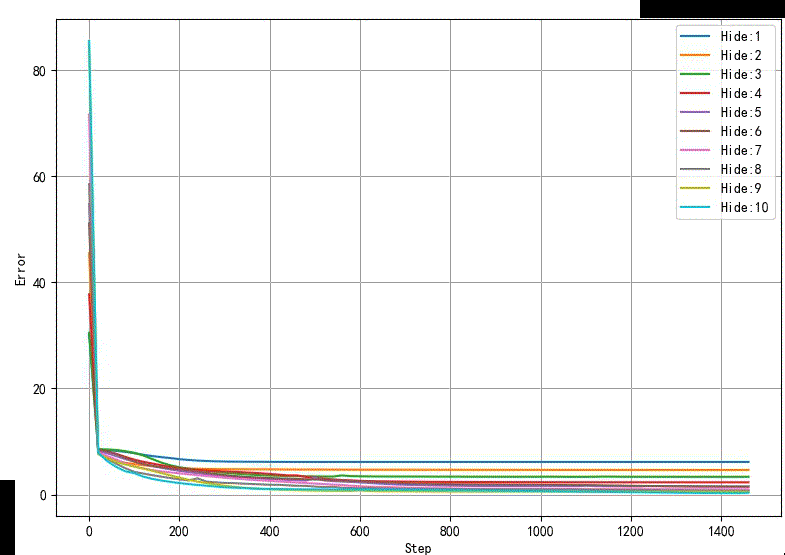
▲ 不同隐层节点网络训练误差收敛情况
下图显示了隐层节点数量与网络在训练2000回合之后变化的情况。
由于样本只有10个,可以看到当隐层节点大于等于10之后,样本回复误差就是0了。
当隐层节点小于10的时候,网络训练误差随着节点的增加而降低。

▲ 隐层节点个数与训练误差
4.学习速率与网络误差
根据前面实验的结果,可以看出,当隐层节点书大于等于10之后,网络的训练误差就非常接近于0了。
下面去网络的隐层节点数目等于10,考察网络学习速率对于网络误差的影响。
设置网络训练次数固定位2000次,绘制出学习速率与网络训练一次(2000周期)对应的误差,如下图所示:

▲ 学习速率与网络误差
从上面的结果看出,学习速率在0.1 ~ 0.2之间,网络学习效果最好。
➤※ 作业1-7中的程序
➤※ 作业程序
1.作业1-7的主程序
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# HW17BP.PY -- by Dr. ZhuoQing 2020-11-19
#
# Note:
#============================================================
from headm import *
from bp1sigmoid import *
A = [0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]
B = [1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
C = [0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
D = [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
E = [1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
F = [1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
G = [0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
H = [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]
I = [0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
J = [0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
x_train = array([A,B,C,D,E,F,G,H,I,J])
y_train = x_train.T
#------------------------------------------------------------
#------------------------------------------------------------
# Define the training
DISP_STEP = 100
#------------------------------------------------------------
pltgif = PlotGIF()
y1dim = []
y2dim = []
y3dim = []
y4dim = []
#------------------------------------------------------------
def train(X, Y, num_iterations, learning_rate, print_cost=False, Hn=10):
n_x = X.shape[1]
n_y = n_x
n_h = Hn
lr = learning_rate
parameters = initialize_parameters(n_x, n_h, n_y)
XX,YY = x_train, y_train #shuffledata(x_train, y_train)
costdim = []
for i in range(0, num_iterations):
A2, cache = forward_propagate(XX, parameters)
cost = calculate_cost(A2, YY, parameters)
grads = backward_propagate(parameters, cache, XX, YY)
parameters = update_parameters(parameters, grads, lr)
if print_cost and i % DISP_STEP == 0:
printf('Cost after iteration:%i: %f'%(i, cost))
costdim.append(cost)
return parameters, costdim
#------------------------------------------------------------
cost_dim = []
Hn_dim = []
Err_dim = []
for i in linspace(0.01, 0.5, 100):
Hn = i + 1
parameter,costdim = train(x_train, y_train, 2000, i, True, 10)
cost_dim.append(costdim)
Hn_dim.append(i)
Err_dim.append(costdim[-1])
tspsave('data', costdim = cost_dim, Hndim=Hn_dim, err=Err_dim)
plt.plot(Hn_dim, Err_dim)
plt.xlabel("Learning Rate")
plt.ylabel("Error")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
# END OF FILE : HW17BP.PY
#============================================================2.BP网络子程序
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# BP1SIGMOID.PY -- by Dr. ZhuoQing 2020-11-17
#
# Note:
#============================================================
from headm import *
#------------------------------------------------------------
# Samples data construction
random.seed(int(time.time()))
#------------------------------------------------------------
def shuffledata(X, Y):
id = list(range(X.shape[0]))
random.shuffle(id)
return X[id], (Y.T[id]).T
#------------------------------------------------------------
# Define and initialization NN
def initialize_parameters(n_x, n_h, n_y):
W1 = random.randn(n_h, n_x) * 0.5 # dot(W1,X.T)
W2 = random.randn(n_y, n_h) * 0.5 # dot(W2,Z1)
b1 = zeros((n_h, 1)) # Column vector
b2 = zeros((n_y, 1)) # Column vector
parameters = {'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return parameters
#------------------------------------------------------------
# Forward propagattion
# X:row->sample;
# Z2:col->sample
def forward_propagate(X, parameters):
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
Z1 = dot(W1, X.T) + b1 # X:row-->sample; Z1:col-->sample
A1 = 1/(1+exp(-Z1))
Z2 = dot(W2, A1) + b2 # Z2:col-->sample
A2 = Z2 # Linear output
cache = {'Z1':Z1,
'A1':A1,
'Z2':Z2,
'A2':A2}
return Z2, cache
#------------------------------------------------------------
# Calculate the cost
# A2,Y: col->sample
def calculate_cost(A2, Y, parameters):
err = [x1-x2 for x1,x2 in zip(A2.T, Y.T)]
cost = [dot(e,e) for e in err]
return mean(cost)
#------------------------------------------------------------
# Backward propagattion
def backward_propagate(parameters, cache, X, Y):
m = X.shape[0] # Number of the samples
W1 = parameters['W1']
W2 = parameters['W2']
A1 = cache['A1']
A2 = cache['A2']
dZ2 = (A2 - Y)
dW2 = dot(dZ2, A1.T) / m
db2 = sum(dZ2, axis=1, keepdims=True) / m
dZ1 = dot(W2.T, dZ2) * (A1 * (1-A1))
dW1 = dot(dZ1, X) / m
db1 = sum(dZ1, axis=1, keepdims=True) / m
grads = {'dW1':dW1,
'db1':db1,
'dW2':dW2,
'db2':db2}
return grads
#------------------------------------------------------------
# Update the parameters
def update_parameters(parameters, grads, learning_rate):
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
dW1 = grads['dW1']
db1 = grads['db1']
dW2 = grads['dW2']
db2 = grads['db2']
W1 = W1 - learning_rate * dW1
W2 = W2 - learning_rate * dW2
b1 = b1 - learning_rate * db1
b2 = b2 - learning_rate * db2
parameters = {'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return parameters
#------------------------------------------------------------
# END OF FILE : BP1SIGMOID.PY
#============================================================





















