作者:凯鲁嘎吉
Deep Embedding Clustering (DEC)和Improved Ceep Emdedding Clustering (IDEC)被相继提出,但关于参数的优化问题,作者并未详细给出,于是乎自己推导了一遍,但是发现和这两篇文章的推导结果不一致,不知道问题出在哪?下面,相当于给出一道数学题,来求解目标函数关于某个参数(以聚类中心为例)的偏导问题。
问题描述
已知
\[L=\sum\limits_{i}^{N}{\sum\limits_{j}^{c}{{{p}_{ij}}\log \frac{{{p}_{ij}}}{{{q}_{ij}}}}}\]
\[{{q}_{ij}}=\frac{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}{\sum\nolimits_{j}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}}\]
\[{{p}_{ij}}=\frac{q_{ij}^{2}/\sum\nolimits_{j}{{{q}_{ij}}}}{\sum\nolimits_{j}{(q_{ij}^{2}/\sum\nolimits_{j}{{{q}_{ij}}})}}\]
固定${p}_{ij}$, 求
\[\frac{\partial L}{\partial {{\mu }_{j}}}\]
问题求解
根据链式法则
\[\frac{\partial L}{\partial {{\mu }_{j}}}=\frac{\partial L}{\partial {{q}_{ij}}}\frac{\partial {{q}_{ij}}}{\partial {{\mu }_{j}}}\]
\[\frac{\partial L}{\partial {{q}_{ij}}}=\frac{\partial \left( {{p}_{ij}}\log \frac{{{p}_{ij}}}{{{q}_{ij}}} \right)}{\partial {{q}_{ij}}}=\frac{\partial \left( {{p}_{ij}}\log {{p}_{ij}}-{{p}_{ij}}\log {{q}_{ij}} \right)}{\partial {{q}_{ij}}}=-\frac{{{p}_{ij}}}{{{q}_{ij}}}\]
\[\frac{{\partial {q_{ij}}}}{{\partial {\mu _j}}} = \sum\limits_i^N {\frac{{\partial \frac{{{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}}}{{\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} }}}}{{\partial {\mu _j}}}} = \sum\limits_i^N {\left( {\frac{{\partial {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}}}{{\partial {\mu _j}}}\frac{1}{{\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} }} + {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}\frac{{\partial \frac{1}{{\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} }}}}{{\partial {\mu _j}}}} \right)} \]
其中
\[\frac{{\partial {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}}}{{\partial {\mu _j}}} = - {(1 + {\left\| {{z_i} - {\mu _j}} \right\|^2})^{ - 2}} \cdot \left( { - 2({z_i} - {\mu _j})} \right) = 2({z_i} - {\mu _j}) \cdot {(1 + {\left\| {{z_i} - {\mu _j}} \right\|^2})^{ - 2}}\]
\[\frac{{\partial \frac{1}{{\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} }}}}{{\partial {\mu _j}}} = - \frac{{2({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 2}}}}{{{{\left( {\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} } \right)}^2}}}\]
所以
\[\frac{{\partial {q_{ij}}}}{{\partial {\mu _j}}} = \sum\limits_i^N {(\frac{{2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 2}}}}{{\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} }} - \frac{{2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 2}} \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}}}{{{{\left( {\sum\nolimits_j {{{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}}} } \right)}^2}}})} = \sum\limits_i^N {\left( {2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}} \cdot {q_{ij}} - 2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}} \cdot q_{ij}^2} \right)} {\rm{ = }}\sum\limits_i^N {\left( {2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}} \cdot {q_{ij}} \cdot (1 - {q_{ij}})} \right)} \]
求导结果
\[\frac{{\partial L}}{{\partial {\mu _j}}} = \frac{{\partial L}}{{\partial {q_{ij}}}}\frac{{\partial {q_{ij}}}}{{\partial {\mu _j}}} = \sum\limits_i^N {\left( { - \frac{{{p_{ij}}}}{{{q_{ij}}}} \cdot 2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}} \cdot {q_{ij}} \cdot (1 - {q_{ij}})} \right)} = \sum\limits_i^N {\left( {2 \cdot ({z_i} - {\mu _j}) \cdot {{(1 + {{\left\| {{z_i} - {\mu _j}} \right\|}^2})}^{ - 1}} \cdot {p_{ij}} \cdot ({q_{ij}} - 1)} \right)} \]
原文结果
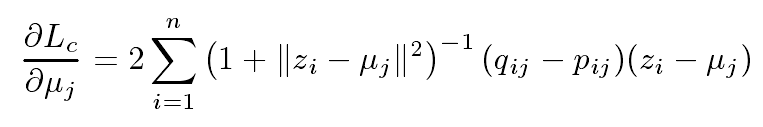
不知道问题出在哪?求广大网友指正~























