旅行传送门
D - Online games
题意:给你 \(n\) 条线段,每条线段的左端点 \(A_i\) 与覆盖长度 \(B_i\) 已知,现让你对每个 \(k \in [1,n]\) ,输出有多少个点被覆盖了 \(k\) 次。
题目分析:如果是暴力做法怎么做?对每条线段 \([A_i,A_i+B_i-1]\) 内的点覆盖次数 \(+1\) ,最后扫一遍整个序列统计每个 \(k\) 值对应的答案。显然无论是时间还是空间都不允许,考虑优化:
首先将每条线段的起始端点 \(A_i\) 和终止端点 \(A_i + B_i\) 存储起来得到一个新序列 \(x\) ,将 \(x\) 按端点大小排序,然后我们再设置一个计数器 \(cnt\) (即图中的 \(k\) )和一个 \(ans\) 数组用来记录答案:
不难发现,每两个端点 \([x_i,x_{i+1}]\) 间的覆盖次数是恒定的,而在从左至右扫的过程中每次遇见端点都会引发 \(cnt\) 的变化,如果当前端点是起始端点,说明对 \(\geq x_i\) 的点覆盖次数 \(+1\) ,即此时对应的 \(cnt\) 值 \(+1\) ,反之亦然。因此两端点之差 \(x_{i+1}-x_i\) 即是对当前 \(k\) 值的贡献。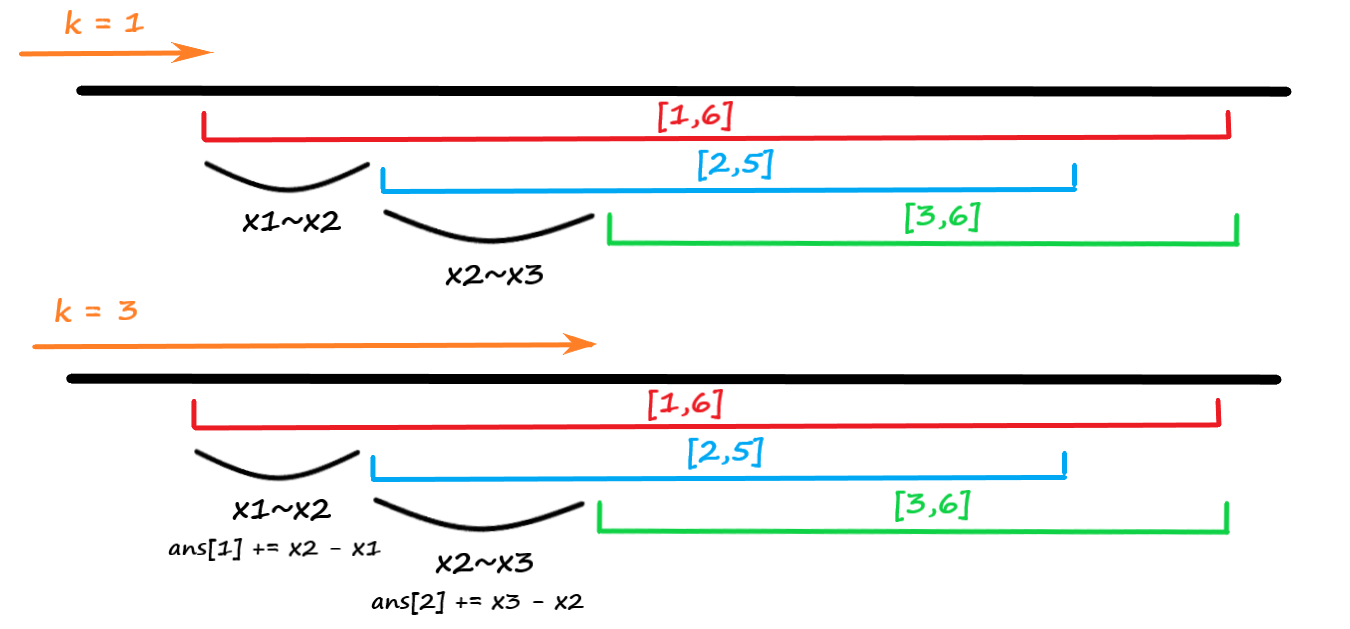

AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i < (y); i++)
#define pii std::pair<int, int>
#define mp std::make_pair
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int main(int argc, char const *argv[])
{
int n = read();
std::vector<int> ans(n + 1);
std::vector<pii> v;
rep(i, 0, n)
{
int a = read(), b = read();
v.push_back(mp(a, 1));
v.push_back(mp(a + b, -1));
}
std::sort(v.begin(), v.end());
int cnt = 0;
rep(i, 0, v.size() - 1)
{
cnt += v[i].second;
ans[cnt] += v[i + 1].first - v[i].first;
}
rep(i, 1, n) printf("%d ", ans[i]);
printf("%d ", ans[n]);
return 0;
}





















