time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
After the piece of a devilish mirror hit the Kay’s eye, he is no longer interested in the beauty of the roses. Now he likes to watch snowflakes.
Once upon a time, he found a huge snowflake that has a form of the tree (connected acyclic graph) consisting of n nodes. The root of tree has index 1. Kay is very interested in the structure of this tree.
After doing some research he formed q queries he is interested in. The i-th query asks to find a centroid of the subtree of the node vi. Your goal is to answer all queries.
Subtree of a node is a part of tree consisting of this node and all it’s descendants (direct or not). In other words, subtree of node v is formed by nodes u, such that node v is present on the path from u to root.
Centroid of a tree (or a subtree) is a node, such that if we erase it from the tree, the maximum size of the connected component will be at least two times smaller than the size of the initial tree (or a subtree).
Input
The first line of the input contains two integers n and q (2 ≤ n ≤ 300 000, 1 ≤ q ≤ 300 000) — the size of the initial tree and the number of queries respectively.
The second line contains n - 1 integer p2, p3, …, pn (1 ≤ pi ≤ n) — the indices of the parents of the nodes from 2 to n. Node 1 is a root of the tree. It’s guaranteed that pi define a correct tree.
Each of the following q lines contain a single integer vi (1 ≤ vi ≤ n) — the index of the node, that define the subtree, for which we want to find a centroid.
Output
For each query print the index of a centroid of the corresponding subtree. If there are many suitable nodes, print any of them. It’s guaranteed, that each subtree has at least one centroid.
Example
Input
7 4
1 1 3 3 5 3
1
2
3
5
Output
3
2
3
6
Note 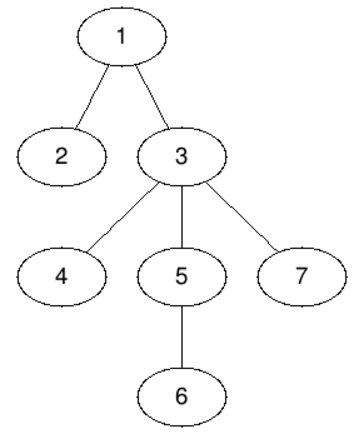
The first query asks for a centroid of the whole tree — this is node 3. If we delete node 3 the tree will split in four components, two of size 1 and two of size 2.
The subtree of the second node consists of this node only, so the answer is 2.
Node 3 is centroid of its own subtree.
The centroids of the subtree of the node 5 are nodes 5 and 6 — both answers are considered correct.
【题解】
这个点就是一棵树的“重心”;
考虑每个节点x。找到它的儿子节点里面以该儿子节点为根的子树的大小最大的点记big;
如果size[big]>(size[x]/2);
则这个子树的重心在big节点下面。
否则这个子树的重心就为x;
->有个性质;
两棵树;
如果通过一条边连成了一棵树;那么新的树的重心一定在原来的两棵树的重心的在新的树的路径上。
则我们找到以big为根的节点的子树的重心,然后不断往上走。找到以x为根节点的树的新的重心。(判断依据看代码);
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 4e5;
int cnt[MAXN], ans[MAXN],fa[MAXN];
int n, q;
vector <int> a[MAXN];
void dfs(int x)
{
cnt[x] = 1;
ans[x] = x;
int len = a[x].size();
int big = 0;
for (int i = 0; i <= len - 1; i++)
{
int y = a[x][i];
dfs(y);
cnt[x] += cnt[y];
if (cnt[y] > cnt[big])
big = y;
}
if (cnt[big] > cnt[x] / 2)
{
int now = ans[big];
int temp = cnt[x] - cnt[now];
while (temp > (cnt[x] / 2))
{
now = fa[now];
temp = cnt[x] - cnt[now];
}
ans[x] = now;
}
}
int main()
{
//freopen("D:\\rush.txt", "r", stdin);
scanf("%d%d", &n, &q);
for (int i = 2; i <= n; i++)
{
int pa;
scanf("%d", &pa);
fa[i] = pa;
a[pa].push_back(i);
}
dfs(1);
for (int i = 1; i <= q; i++)
{
int x;
scanf("%d", &x);
printf("%d\n", ans[x]);
}
return 0;
}




















