You've got an array a, consisting of n integers a1, a2, ..., an. You are allowed to perform two operations on this array:
- Calculate the sum of current array elements on the segment [l, r], that is, count value al + al + 1 + ... + ar.
- Apply the xor operation with a given number x to each array element on the segment [l, r], that is, execute
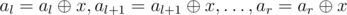. This operation changes exactly r - l + 1 array elements.
Expression 
means applying bitwise xor operation to numbers x and y. The given operation exists in all modern programming languages, for example in language C++and Java it is marked as "^", in Pascal — as "xor".
You've got a list of m operations of the indicated type. Your task is to perform all given operations, for each sum query you should print the result you get.
Input
The first line contains integer n (1 ≤ n ≤ 105) — the size of the array. The second line contains space-separated integers a1, a2, ..., an (0 ≤ ai ≤ 106) — the original array.
The third line contains integer m (1 ≤ m ≤ 5·104) — the number of operations with the array. The i-th of the following m lines first contains an integer ti (1 ≤ ti ≤ 2) — the type of the i-th query. If ti = 1, then this is the query of the sum, if ti = 2, then this is the query to change array elements. If the i-th operation is of type 1, then next follow two integers li, ri (1 ≤ li ≤ ri ≤ n). If the i-th operation is of type 2, then next follow three integers li, ri, xi (1 ≤ li ≤ ri ≤ n, 1 ≤ xi ≤ 106). The numbers on the lines are separated by single spaces.
Output
For each query of type 1 print in a single line the sum of numbers on the given segment. Print the answers to the queries in the order in which the queries go in the input.
Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams, or the %I64d specifier.
Examples
Input
Output
Input
Output
题意：
ｎ个数，两个操作，
１.查询ａ［ｌ～ｒ］的和
２.ａ［ｌ～ｒ］都异或ｘ
分析：
当x的某一位为1，区间中所有a[ i ]所有为1的要变为0，为0的变为1，然而当其为0时，a[i]对应位是0或者1对答案均无影响 ；
线段树维护一个数组ｄｉｇｔ，保存的是这个区间中在第ｉ位置上为１的个数。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
#define lson i<<1
#define rson i<<1|1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define ll long long
#define N 100005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define lowbit(x) (x&-x)
int b[N];
ll ans_sum,ans_max,ans_min;
//注意一定要找一个临时变量记录下ans_***的答案，不然会覆盖
struct node
{
int l,r;
int dig[32];
int lazy;
} tree[N<<2];
void pushdown(int i,int l,int r)//标记下传
{
if(tree[i].lazy)
{
tree[lson].lazy^=tree[i].lazy;
tree[rson].lazy^=tree[i].lazy;
int mid=(l+r)/2;
for(int j=0; j<25; j++)
{
if((tree[i].lazy>>j)&1)
{
tree[lson].dig[j]=mid-l+1-tree[lson].dig[j];
tree[rson].dig[j]=r-mid- tree[rson].dig[j];
}
}
tree[i].lazy=0;
}
}
void pushup(int i)
{
for(int j=0; j<25; j++)
{
tree[i].dig[j]=tree[lson].dig[j]+tree[rson].dig[j];
}
}
//建立线段树
void build(int l,int r,int i)
{
tree[i].l = l;
tree[i].r = r;
tree[i].lazy = 0;
if(l == r)
{
for(int j=0; j<25; j++)
{
if((b[l]>>j)&1)
tree[i].dig[j]=1;
else
tree[i].dig[j]=0;
}
return;
}
int mid = (l+r)>>1;
build(LS);
build(RS);
pushup(i);
}
//tree[l,r]+=val
void xor_data(int l,int r,int i,int val)
{
if(tree[i].l>=l&&tree[i].r<=r)
{
tree[i].lazy^=val;
for(int j=0; j<25; j++)
{
if((val>>j)&1)
{
tree[i].dig[j]=tree[i].r-tree[i].l+1-tree[i].dig[j];
}
}
return;
}
pushdown(i,tree[i].l,tree[i].r);//标记下传
int mid = (tree[i].l+tree[i].r)>>1;
if(l<=mid)
xor_data(l,r,lson,val);
if(r>mid)
xor_data(l,r,rson,val);
pushup(i);
}
void query(int l,int r,int i)
{
if(l <= tree[i].l && tree[i].r <= r)
{
for(int j=0; j<25; j++)
{
ans_sum+=(LL)tree[i].dig[j]*((1LL)<<j);
}
return ;
}
// cout<<l<<" "<<r<<endl;
pushdown(i,tree[i].l,tree[i].r);
int mid = (tree[i].l+tree[i].r)>>1;
if(l<=mid)
query(l,r,lson);
if(r>mid)
query(l,r,rson);
pushup(i);
}
int main()
{
int n,m;
while(scanf("%d",&n)!=-1)
{
for (int i=1; i<=n; i++)
{
scanf("%d",&b[i]);
}
build(1,n,1);
scanf("%d",&m);
for(int i=1; i<=m; i++)
{
int op;
int l,r,x;
scanf("%d",&op);
if(op==1)
{
scanf("%d%d",&l,&r);
ans_sum=0;
query(l,r,1);
printf("%lld\n",ans_sum);
}
else
{
scanf("%d%d%d",&l,&r,&x);
xor_data(l,r,1,x);
}
}
}
return 0;
}
