processing 写的规律图形运动
也是第一次用processing写图形,期间参考了别人的做法,废话不多说,直接开始
我原本是准备完成这一张图

不过做的途中出现了点问题,然后我又想实现点花里胡哨的的效果,结果就变成了这个样子
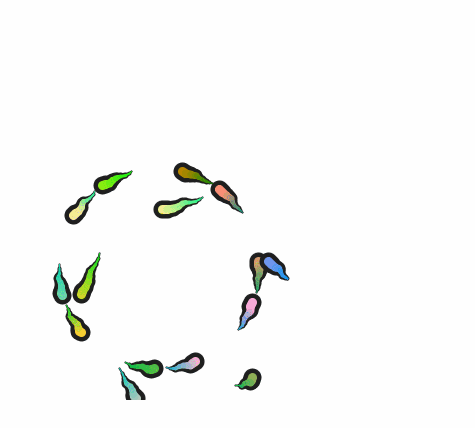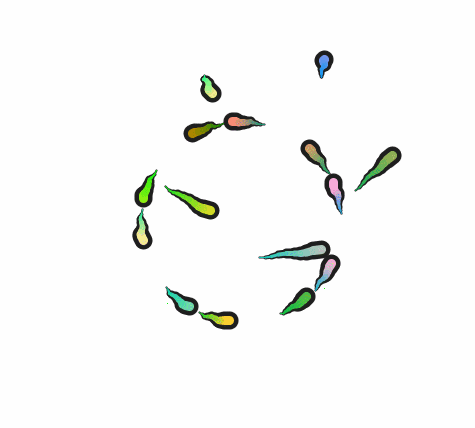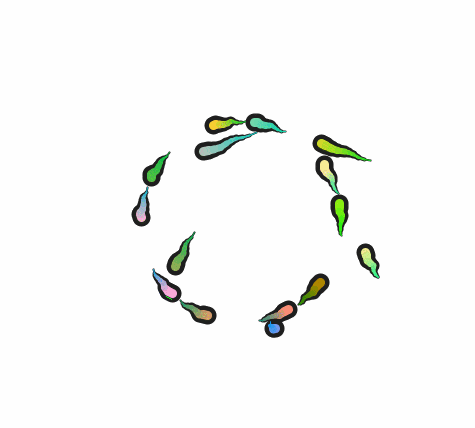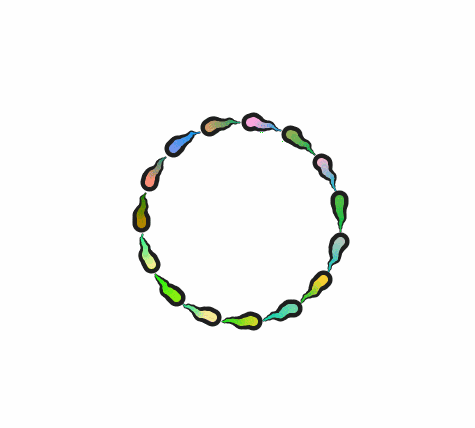
好的,我知道这两个完全不像,其实是我数学有点算不明白。
下面一点一点说明
原图分析:第一个图实际上有这么几个方面
1.旋转
2.旋转的同时,每个点都在沿着直线简谐运动
3.时间要卡的很准,否则就是混乱的
4.运动模糊
接下来是我做的过程
我不喜欢模糊的感觉,我喜欢拖尾的感觉,然后查找别人的代码,知道了大概点运动的时候拖尾,而且是两层该怎么处理(一层是黑,一层是变色)。
刚开始我是考虑拖尾的问题,喜欢研究这些花哨的。
这样实现的。
class Particle {
ArrayList points = new ArrayList();void draw(int k) {
stroke(30);
for (int i = points.size()-1; i > 0; i–) {
PVector l = points.get(i);
PVector l2 = points.get(i-1);
strokeWeight(map(i, 0, points.size(), 0, 20));
line(l.x, l.y, l2.x, l2.y);
}
//hei
for (int i = points.size()-1; i > 0; i–) {
PVector l = points.get(i);
PVector l2 = points.get(i-1);
stroke(map(i, points.size()-1, 0, k20%255+80, 0), 255-k, k17%255);
strokeWeight(map(i, 0, points.size(), 0, 10));
line(l.x, l.y, l2.x, l2.y);
}//hong
}void move(PVector loc) {
points.add(loc);
if (points.size() > 10) {
points.remove(0);
}
}
}
这个是点的定义,这个拖尾的主要方式就是把点连成线,然后点的大小和颜色改变,做成水滴的感觉(不过上面那是蝌蚪的感觉,我会说明为啥的)
下面是线的定义,就是如何排列这一个一个点。
class Link {
Particle p;int i;
Link(int i) {
this.i = i;
p = new Particle();
// p2 = new Particle();
}void draw(int k) {
p.draw(k);
// p2.draw();
}
//100sin(frameCount)
void move() {
PVector loc;
if((t/180)%2==1 && ((i/24)==0 || (i/24)==3 || (i/24)==6 || (i/24)==9 || (i/24)==12|| (i/24)==15)){
loc = new PVector(sin(PI/180(i+frameCount2))100+100sin(PIframeCount/180)cos(PIframeCount/90+12), cos(PI/180*(i+frameCount2))100+100sin(PIframeCount/90)sin(PIframeCount/180+12));}
else{
loc = new PVector(sin(PI/180*(i+frameCount2))100, cos(PI/180(i+frameCount2))100);
}
p.move(new PVector(loc.x+sin(5frameCount), loc.y+cos(5frameCount)));
// p2.move(new PVector(loc.x-sin(radians(i))50, loc.y-cos(radians(i))50));
//100cos(radians(2frameCount+i))sin(radians(2frameCount+i)),+100cos(radians(2*frameCount+i))cos(radians(2frameCount+i))
//(t/180)%2==1
}
}
这个是线的处理,里面的重要的函数的意思,和数学的意思我会在接下来讲。
不同的点的颜色的处理,以及每个水滴的颜色包括每个颜色的内部都不太一样是因为这一句。
stroke(map(i, points.size()-1, 0, k20%255+80, 0), 255-k, k17%255);
里面的k是我在之前设定的一个变量,每个水滴的k都不一样。map就是把一段数字映射到另一段数字上。上面的rgb值都是我瞎试的,发现这个方式做出来确实是挺随机的,关键还不是random那种乱七八糟的随机,是有规律的,那相连的点的颜色就会是渐变的。
strokeWeight(map(i, 0, points.size(), 0, 10));
这句话当然就是改变每个点的大小了,头大尾小的水滴就是这样了,i是我之前定义的每个初始点的度数,基本就是代表是哪个点了。
下面是蝌蚪的实现
p.move(new PVector(loc.x+sin(5frameCount), loc.y+cos(5frameCount)));
简单的说就是在算出点的坐标后给个圆,就神奇的发现他在绕着圈抖。
最难的部分就是数学这里了。就是这一段的得来
if((t/180)%2==1 && ((i/24)==0 || (i/24)==3 || (i/24)==6 || (i/24)==9 || (i/24)==12|| (i/24)==15)){
loc = new PVector(sin(PI/180*(i+frameCount2))100+100sin(PIframeCount/180)cos(PIframeCount/90+12), cos(PI/180*(i+frameCount2))100+100sin(PIframeCount/90)sin(PIframeCount/180+12));
}
else{
loc = new PVector(sin(PI/180*(i+frameCount2))100, cos(PI/180(i+frameCount2))*100);
}
每个数字都是经过计算的,否则运动过程中一定有地方不对
开头的if是每180帧可以绕圈转,然后180帧有五个蝌蚪开始转,然后绕一圈后愉快的回归大家庭中,我是有15个点,所以每个点都隔24°。我一直想计算出个表达式让他的点可以一个一个运动出来,但是每次的结果都不对,但是实际上每次的结果还都挺漂亮的。
我之前还想过,只让点简谐运动,不让他旋转,让画布旋转,后来我放弃了这个想法,因为画布旋转的话可以实现这个效果,但是这就让蝌蚪沿着圆走的时候没有了拖尾,因为蝌蚪实际上没动,是画布旋转的。





















