为了使数据有更强的可读性,使人们更好地理解和解释数据,利用表格法和图示法来组织和汇总数据是很好的选择
下图是对表格法和图示法组织数据方式的汇总

下面重点介绍其中几个方法
茎叶图
茎叶图属于探索性数据分析,该技术可以同时显示等级顺序和数据集的形状
茎叶图有两个优势:1)利于手绘 2)可以在图形中包含具体数据的数值

交叉分组表
交叉分组表的主要价值在于它提供了变量间关系的深刻含义
例如下图为300家饭店的质量等级和餐价的交叉分组表(可以由EXCEL的数据透视表生成)

但是在利用交叉分组表时需要小心,这里涉及到辛普森悖论
下面举个辛普森悖论的例子:
“校长,不好了,有很多男生在校门口抗议,他们说今年研究所女生录取率42%是男生21%的两倍,我们学校遴选学生有性别歧视”,校长满脸疑惑的问秘书:“我不是特别交代,今年要尽量提升男生录取率以免落人口实吗?”
秘书赶紧回答说:“确实有交代下去,我刚刚也查过,的确是有注意到,今年法学院录取率是男性75%,女性只有49%;而商学院录取率是男性10%,女性为5%。二个学院都是男生录取率比较高,校长这是我作的调查报告。”
学院 | 女生 申请 | 女生 录取 | 女生 录取率 | 男生 申请 | 男生 录取 | 男生 录取率 | 合计 申请 | 合计 录取 | 合计 录取率 |
商学院 | 100 | 49 | 49% | 20 | 15 | 75% | 120 | 64 | 53.3% |
法学院 | 20 | 1 | 5% | 100 | 10 | 10% | 120 | 11 | 9.2% |
总计 | 120 | 50 | 42% | 120 | 25 | 21% | 240 | 75 | 31.3% |
“秘书,你知道为什么个别录取率男皆大于女,但是总体录取率男却远小于女吗?”
此例这就是统计上著名的辛普森悖论(Simpson's Paradox)
隐藏变量
例如上例中的隐藏变量就是“学院”,当我们将学院这一变量引入分析后就能使问题更加清楚而避免产生不必要的麻烦。
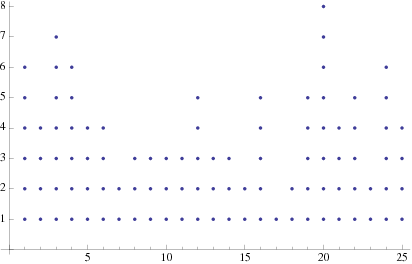
打点图(dot plot)
一种汇总数据的图形方法,用横轴上的点代表每一个数值,通过点的个数来显示数据值的分布情况(如下图所示)