数据结构:把数据放入结构里,通过结构里最基本的计算方法(增、删、改、查)操作数据。
是什么
编程要想写好程序,就需要学习数据结构;可数据结构是什么呢,我们以画画来举个例子。
一般人画画通常就直接画 --- 如画水里的两条金鱼就直接从某一个部分开始,从外形画起来了。
一般人的画法结果经常是,画到后来比例不对,而且常常画得不像;而专业人士就是画什么像什么、细节特别突出!!!
专业人士又是如何做到的呢 ???
百思不得其解,先看看梵高的作品吧(素描):

就是那个画向日葵的梵高。

问一下才明白,专业人士画的画都讲究框架。

这是初中美术书上的《美杜莎之伐》,美术书上还有一副设计初稿:

这副画最高层的构图设计就是俩个金字塔形状,《美杜莎之伐》就是靠着俩个三角形的金字塔,画面保持了平衡。
那么,您再看看梵高的作品,能不能看出什么呢 ?
除了画画之外,我们学习写作不也讲究结构,像总分总......
专业画家画画,他们会把金鱼分解成几个简单的几何图形
对于编程来说,写一个能够完成特定功能的程序,就相当于是作一幅画、一篇文章。
因此,也有两种方法,
- 一般人编程:直接就用一行行代码去实现功能,这是低水平的做法,有些时候看上去做得快,实际上Bug多,回头需要修补;
- 专业人士写:理解需求之后,抽象出作品需要的基本几何图形,而后用算法将这些模块进行组合,写出符合需求的程序。
这些基本模块也像绘画和文章中作为轮廓的几何图形一样,需要根据画面需求平滑过渡,而不是照搬照抄。
这些程序中基本的几何图形,就是计算机的数据结构。
基本的几何图形有(一系列的点被连成了一种规则的形状):
- 三角形
- 长方形
- 金字塔形
- 圆形
- 椭圆形
编程也有基础结构(一系列的数据被组织为一种抽象的形状):
- 集合
- 线性表
- 树
- 图
数据就等同于点,数据结构就是点中常用的具体关系。
历史
第一种数据结构是集合,因为计算机起源于数学,所以数据结构也有数学部分的。
集合,就是我们数学上定义的,也是高中数学里学过的。
集合在数据结构中一般只是一个辅助,是某个复杂的数据结构的一部分。
集合的特点是元素分类且不重复。
第二种数据结构是线性表,这相当于几何图形中的直线,也是最基本的数据结构。
线性表这种抽象的数据结构并非起源于科学计算本身,而是计算机早期的应用——办公自动化。
我们知道,虽然发明计算机的目的是为了科学计算,但是TA最早期的商业应用则是在管理和商业方面。
在商业上,报表是一种最常见的数据组织形式,而在管理上,最多见的则是人员或者物资的记录等等。
TA们都可以被抽象为线性的数据,然后按照 1、2、3、4、5 的顺序排列出来。
比如一所大学所有学生的档案,就是这样一个个按照顺序排列的,而他们的编号就是学号。
因此,很有必要设计一种抽象的数据结构概括所有这些顺序排列和储存的数据,TA就是线性表。
当然,随着计算机数据规模的扩张,未必能够给所有的数据都赋予一个编号顺序,结构化地存储,但是TA们依然遵循一个顺序的特征。
比如一个电商交易的日志记录,TA是按照所发生的时间顺序,一条条线性地记录下来,因此,线性表的性质TA们也有。
实现线性表的方法有三种:
- 数组
- 链表
- 散列
线性表结构关系是一对一。
第三种数据结构是树。
计算机科学家们正面临着一个大问题:在我们真实的世界里,到底是具体的数值重要,还是数值之间相对的大小更重要,或者说相对的次序更重要?
相对大小:在物理上,水的冰点不到 0 度是无法结冰的;
相对次序:在编程里,AlphaGo 和别人下棋的时候经常会说,这一步棋可以赢取了多少目,可AlphaGo 却不走 ?这是因为计算机只看相对的输赢,所以才走一步稳妥。
在计算机中,由于经常要做的事情是判断真假、比较大小、排序、挑选最大值这类的操作,而它们在计算机的世界里又如此重要,所以相对次序比相对大小更重要;于是计算机科学家们专门设计一种数据结构,这种数据结构被称为二叉树。
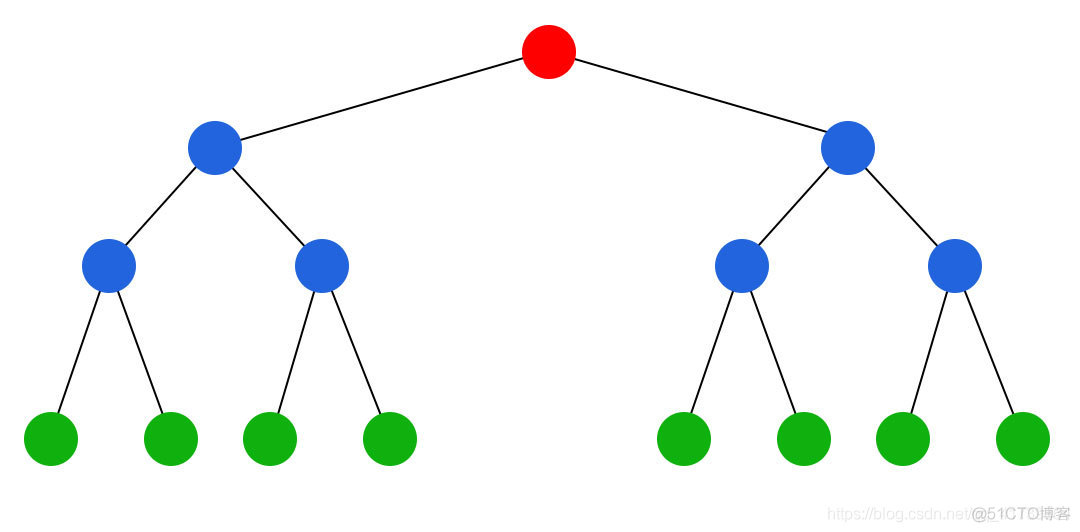
二叉树都有一个根,二叉树的根就是图中顶上红色的那个点。
这是为了将来把二叉树一层层扩展,二叉树的根画在了最顶端,而不是下面,您把自然界的大树转180度就可以了。
从根开始都有分叉,只不过二叉树为了简单起见,只能有两个分叉,不能更多,这一点和自然界的树不同。
每一个分叉也有一个自己的根结点,就是图中蓝色的那些点,可以把TA们想象成大树各级主干分叉前的部分。
当然,您可能会问,如果遇到一个特殊的问题,需要三个分支怎么办?
在数学上,两个分支和 N 个分支是等价的,或者说 N 个分支的情况可以通过俩个分支来实现。
因此,为了简单起见,也为了更好的通用性,我们只研究二叉树就可以了。
最后,我们知道一棵树的树杈还能再分叉,二叉树也是如此,任何一个枝杈都可以再分出两枝,这个过程可以无限持续下去。
二叉树虽然是一种抽象的东西,在自然界中并不存在,但是它却浓缩了自然界很多事物的共性,那就是分叉、层层递进和有序。而针对这些共性,科学家们又总结出一些具有普遍性的算法,能够回过头来,应用到各种实际问题中。
树的结构关系是一对多。
树主要分成俩类:二叉树和非二叉树。
- 二叉树:二叉树、堆、AVL树、红黑树、默克尔树。
- 非二叉树:B树、哈夫曼树、字典树、线段树、伸展树、VEB树、哈希树、KD树、区间树、B+树、rang Tree、并查集、SBT树、斯坦纳树、2-3树、cover Tree、insider Tree。
第四种数据结构是图。
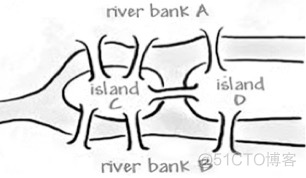
图这种数据结构起源于大数学家欧拉。
这是小学数学书上的一道题,好像是二年级..... (我当初试过,所以印象深刻)
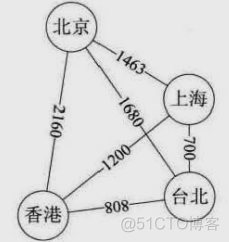
图论是生活中的一个抽象的概念或者说是工具,围绕图,计算机科学家们设计了很多算法,然后把很多实际问题抽象出来,用图论的算法解决。
关于图的算法有很多,但最重要的是图的遍历算法,也就是如何从一个点出发,通过连接的线访问图的各个点。
具体的数学推导,可以看看博文《爬虫导论|如何下载整个互联网的网页》。
图要是学好了,您可以跨学科研究:社会网络、数据分析、离散数学、网络爬虫、道路规划、机器人导航......
图的结构关系是多对多。
图主要是算法:
- 搜索算法:遍历树、BFS、DFS、剪枝、双向BFS、启发式搜索
- 匹配问题:最大流、匈牙利
- 最短路径:动态规划设计思路、Dijkstra、Bellman-Ford、Floyd、A*、JohnSon、Spfa
- 最小生成树:切分定理、Kruskal、Prim、Gabow+Spfa、BottleNeck、MstReucePrim、SecondaryMSt、Fredman-Tarjan、Chazelle
- 有向图算法:拓扑排序、强联通分量
- 网络流:Ford Fulkerson框架、Edmonds-Kap 、Dinic、MPM、标签ISPA、HopcaraftKarp、最大流最小割
- 离散数学:欧拉路径/回路、哈密尔顿路径/回路
- 关键路径:AOE网
扩展:图论专题的《图的大致介绍》。
线性表、树、图是数据结构这门学科的主线:
- 一些计算机科学家求多,他们认为想要更多的功能,就需要更多的结构,关注的是结构的面值。
比如,链表捣鼓了多个版本,如单向链表、双向链表、循环链表。
引入了 矩阵、字符串、哈希表 等结构。
或者是通过基础的顺序存储结构和链式存储结构搭积木式组合形成了新的结构。
还有排序和查找、各种算法设计思想(如递归)、各个领域的算法(如数论、计算几何、图论)、AI算法(如遗传算法)。
求多,越多越好,想要更多的功能,就需要更多的结构。
- 另一些计算机科学家俭省,他们认为结构本身是一回事,而人怎么利用这个结构是另一回事。如果人能够善加利用,就可以给任何结构创造新的价值。利用少的结构,获取更多的功能,一个结构到了您的手里,您能不能给TA增加一点创造性的附加值。
他们给当前的结构设定了一个限制,逼着自己在一个框架之内寻找发挥,专注于给已有的结构开发新用途。
从这种视角来看,线性表、树、图都是一个东西,线性表是一种受限制的树,树是一种受限制的图,可以说都是图。
通过限制线性表,得到了新的逻辑结构:栈、队列、堆。
俭省,不需要太多,释放少的潜能,取得多的成就。
区别
数据结构、数据类型,我经常分不清,特别是 C语言里面需要自己实现的数据结构怎么到了 Python 就变成了数据类型,他们是啥关系?
比如,我准备盖栋房子:
- 需要各种已经做好并组合的物件,ta是房子的骨架,ta也是程序中的数据结构。
- 当使用各种不同尺寸和标号的钢筋,如,按直径分,钢丝(直径3~5mm)、细钢筋(直径6~10mm)、粗钢筋(直径大于22mm),这些钢筋即程序中的数据类型,做横梁也许用10mm的钢筋,做楼梯也许用22mm的钢筋,这和程序的 int 与 unsigned int 类似。
其实数据结构还是数据结构,只不过有些高级语言为了方便编程,把数据结构封装好了,不用重复造轮子。
资料
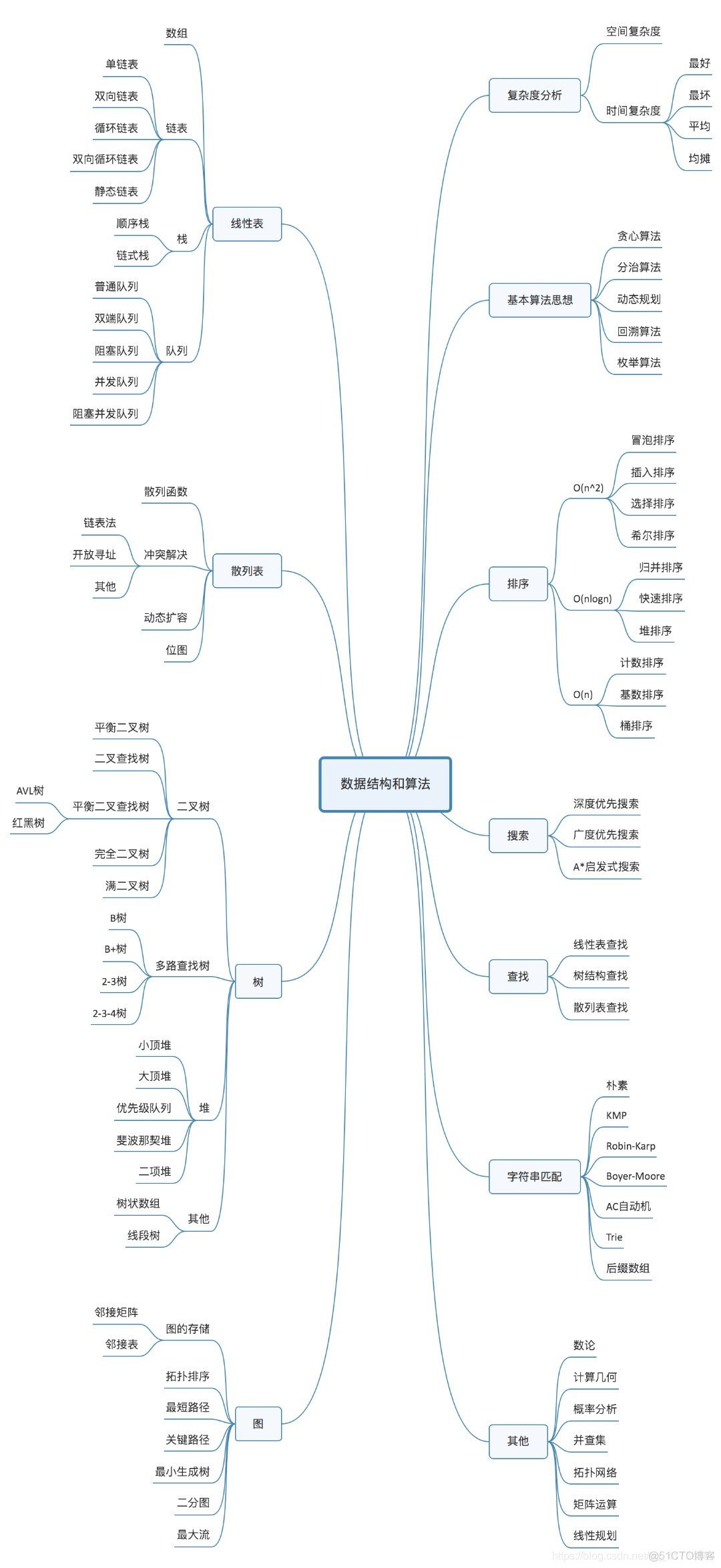
数据结构,推荐从《大话数据结构》开始:
- 学的线性表的时候,补充《漫画算法:小灰的算法之旅》
- 学到树、图的时候,补充《啊哈算法》
- 学算法的时候,多做算法题,具体可以查看《算法训练:嘘,别人我不告诉TA》、《Leetcode题解索引》
- 想学好树的时候,补充《高级数据结构》
- 如果想可视化线性表、树、图,看一下 dot 语言的资料即可,很简单的,可以操作文件的编程语言都可以画出来。
二叉树可视化[C 操作 dot]:
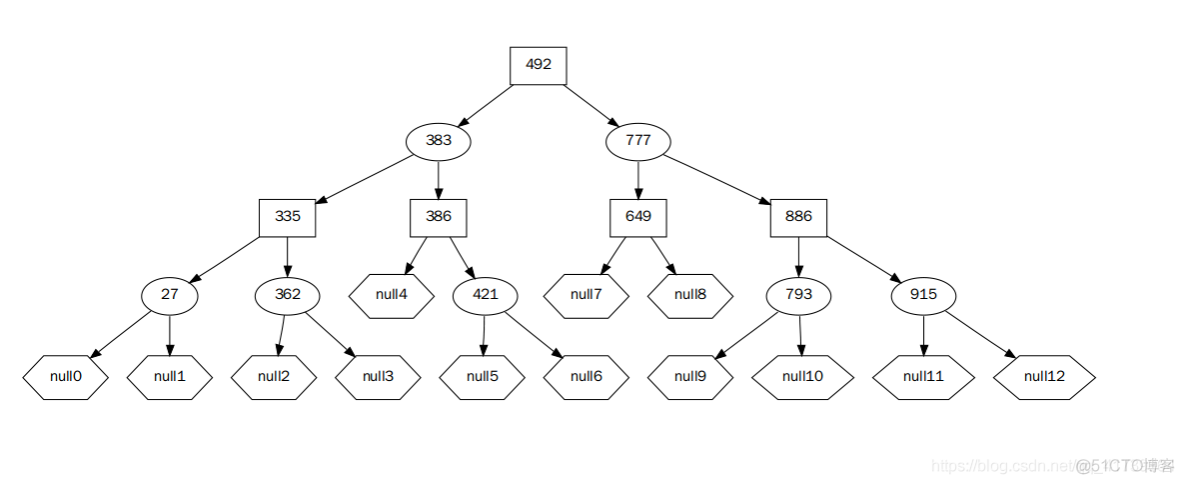
- dot 语言可视化,具体请见《图的分类与建模、跨语言可视化》。
- 数据结构可视化:https://visualgo.net/en
- 算法可视化:https://algorithm-visualizer.org/backtracking/hamiltonean-cycles
数据结构往往是和算法一起的,数据结构与算法这门课,难点也就是在算法上。
算法训练,可以参考另一篇:
- 《算法训练:嘘,别人我不告诉TA》
这篇文章,是不是有什么不可告人的密秘呢!!值得一看。