bfs dfs 公式java java bfs和dfs

Java算法之dfs 与bfs

• 1. dfs

• 1.1 dfs递归
• 
  

• 2. bfs

• 1. bfs常见两类问题

• 1.1==是否==有路径问题
• 1.2最短路径问题

• 2.1迷宫问题：
• 2.2==还原==路径

1. dfs

深度优先遍历(Depth First Search, 简称 DFS)
深度优先遍历各个节点，需要使用到栈（Stack）这种数据结构。Stack的特点是是先进后出，首先将右节点压入栈中，在将左节点压入栈中，这样出栈顺序就是先左节点再右节点。
DFS是图论里面的一种搜索算法，他可以由一个根节点出发，遍历所有的子节点，进而把图中所有的可以构成树的集合都搜索一遍，达到全局搜索的目的。所以很多问题都可以用dfs来遍历每一种情况，从而得出最优解，但由于时间复杂度太高，我们也叫做暴力搜索。

一张动图了解dfs与bfs区别：

dfs序为：1—>2—>3—>2—>1—>4—>5—>6—>5—>4—>7—>4—>1—>8—>9—>8—>1

1.1 dfs递归

递归必须具备两个条件，一个是调用自己，一个是有终止条件。这两个条件必须同时具备，且一个都不能少。并且终止条件必须是在递归最开始的地方，下面是基本模板(｡･ω･｡)ﾉ♡

public class newText2 {
    public static void main(String[] args) {
        dfs( step );
    }
    static void dfs(int step) {
       
        if (暴搜结束的条件)  //
        {
            System.out.println(输出题目答案);
            return ; //结束
        }
        
        if (x >= n) return;  //判断边界
        
        for ( i=1; i<=n; i++) //尝试每一种可能
        { 
		     dfs(step+1) //继续下一步
		}
    }
}

现在你已经了解dfs了，来实战吧( ૢ⁼̴̤̆ ㉨ ⁼̴̤̆ ૢ)♡

在一个给定形状的棋盘（形状可能是不规则的）上面摆放棋子，棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列，请编程求解对于给定形状和大小的棋盘，摆放k个棋子的所有可行的摆放方案总数。
输入
4 4
…#
…#.
.#…
#…
Sample Output
1

思路：
棋子只能放在#上并且 k 个棋子必须在不同行不同列，所以说这里 进行了状态的限制，我们如果用B F S 做肯定不太好做，但是我们刚好可以运用D F S 的回溯特点做这个题目;
定义一个数组V I S [i]，它标记着第i列有没有放棋子，如果第 i 列放了棋子，那么我们就令 v i s [ i ] == true 。

import java.util.*;
import java.util.Scanner;
public class newText2 {
    public static void main(String[] args) {
        Text draw = new Text();
        Scanner mc = new Scanner(System.in);
        int n = mc.nextInt();//总行数
        int k = mc.nextInt();//要放几个棋子
        char[][] mp = new char[n][];  //棋盘
        String t = mc.nextLine();
        for (int j = 0; j < n; j++) {  //输入棋盘
            String s = mc.nextLine();
            mp[j] = s.toCharArray();
        }
        draw.dfs(0, 0, mp, n, k);
        System.out.println(draw.cnt);
    }

    static class Text {
       
       int cnt = 0;
       
        void dfs(int x, int way, char[][] mp, int n, int k) {//用way记录我们放了多少棋子
        boolean[] vis = new boolean[n];//标记每一列
            if (way == k) {
                cnt++;//cnt记录方案数
                return;//一定记得要return
            }
            if (x >= n) return;//这是判界，一共有n行不能多出去
            for (int i = 0; i <  mp[x].length; i++) {//判断这一行的每一列
                if (mp[x][i] == '#' && !vis[i]) {//如果说这mp[x][i]刚好是# 而且第i列是 false没有放棋子
                    vis[i] = true;//我们就放上，并作标记
                    dfs(x + 1, way + 1, mp, n, k);//在下一行放，这一行已经无法放了，不同行不同列
                    vis[i] = false;//此处为回溯的关键点，有疑问的话，请看下图分解
                }
            }
            dfs(x + 1, way, mp, n, k);//这一行找不到的话就直接进行下一行
        }
    }
}

到这里，友友们可能会有些许疑问,下面举个2*3棋盘, 放置2个棋子为例。

#	0	#
0	0	0

dfs(x + 1, way + 1);//在下一行放，这一行已经无法放了，步骤 一
vis[i] = false;//此处为回溯的关键点， 步骤 二

dfs在执行到步骤一时，因为自己调用自己，会一直连续“套娃”，直到出界触发 return, 才会执行步骤二，如下图：

#	1	#
1	#	0

取到第二个数时 for 循环 i=0，接着执行步骤二 vis[i] = false取消标记;for循环继续i=1,i=2。直到找到空位，否则就到下一行(出界触发 return)
当第一个数的情况都遍历完，此时第一个数的 i=1，for循环继续遍历i=2，
由于 vis[i] = false取消标记，使i=2遍历正常进行。

递归的好处：代码更简洁明了，可读性更好。
实际上递归的代码更清晰，一般来说，一个人可能很容易的写出前中后序的二叉树遍历的递归算法，要写出相应的非递归算法就比较考验水平了。所以说递归代码更简洁明了。

递归坏处：由于递归需要系统堆栈，所以空间消耗要比非递归代码要大很多。而且，如果递归深度太大，超出递归的最大深度，系统可能撑不住

2. bfs

广度优先遍历(Breath First Search简称 BFS)，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。

上文所述树的广度优先遍历动图如下，每个节点的值即为它们的遍历顺序。所以广度优先遍历也叫层序遍历，先遍历第一层(节点 1)，再遍历第二层(节点 2，3，4)，第三层(5，6，7，8)，第四层(9，10)。

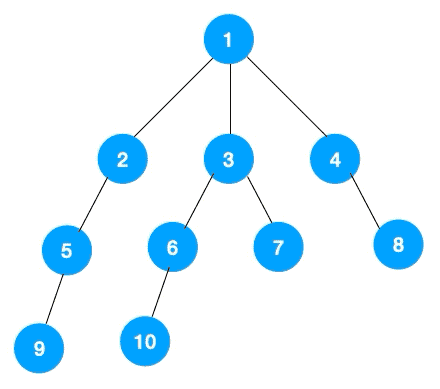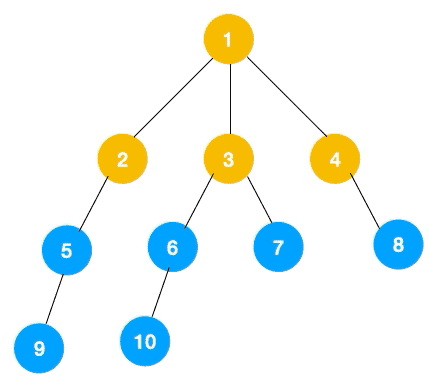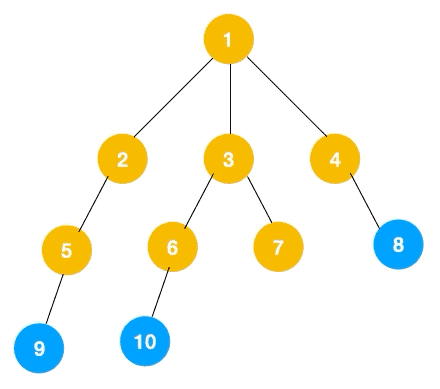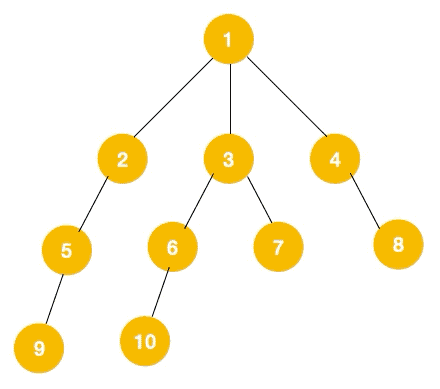
深度优先遍历用的是栈，而广度优先遍历需要用到队列（Queue）来存储节点对象，队列的特点就是先进先出。先往队列中插入左节点，再插入右节点，队列出队就是先出左节点，再出右节点。

队列来实现广度优先遍历，动图如下：

广度优先搜索可回答两类问题。

❑ 第一类问题：从节点A出发，有前往节点B的路径吗？( 是否有路径问题）

❑ 第二类问题：从节点A出发，前往节点B的哪条路径最短？( 最短路径问题)

1. bfs常见两类问题

1.1是否有路径问题

倒水问题：

有两个水壶，容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 targetCapacity 升。
如果可以得到 targetCapacity 升水，最后请用以上水壶中的一或两个来盛放取得的 targetCapacity 升水。
你可以：
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水，直到装满或者倒空

示例 1:
 输入: jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
 输出: true
 .
 示例 2:
 输入: jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
 输出: false
 .
 示例 3:
 输入: jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
 输出: true
 .
 提示:
 1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106

思路：
注意到这道题操作水壶的时候，两个水壶不可能同时都是半满的。如果某个水壶是半满的，另外一个肯定是满的或者空的。而且如果某个水壶是半满的（此时另外一个就是空的或者满的），就不能直接把这个水壶填满，也不能把这个半满的水倒掉，因为这会回到初始状态，这么做没有意义。
允许：
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水，直到装满或者倒空
即六种操作：
// 把 X 壶灌满
// 把 Y 壶灌满
// 把 X 壶倒空
// 把 Y 壶倒空
// 把 X 壶的水灌进 Y 壶，直至灌满或倒空
// 把 Y 壶的水灌进 X 壶，直至灌满或倒空。

import java.lang.*;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class newText2 {
    public static void main(String[] args) {
        Scanner mc=new Scanner(System.in);
        int x = mc.nextInt(); //分别输入两个瓶子的容积
        int y = mc.nextInt();
        int z = mc.nextInt();
        Solution sou =new Solution();
        System.out.println(sou.canMeasureWater(x,y,z));

    }
    static class Solution {
        public boolean canMeasureWater(int x, int y, int z) {

            Queue<int[]> Queue = new LinkedList<int[]>(); //广度优先遍历使用队列
            Queue.add(new int[]{0, 0}); //添加
            Set<Long> seen = new HashSet<Long>(); //long 用于保存长类型数据
            while (!Queue.isEmpty()) {
                if (seen.contains(hash(Queue.peek()))) {  //哈希查重
                    Queue.poll();  //删除队头元素
                    continue;
                }
                seen.add(hash(Queue.peek())); //无重复则 添加

                int[] state = Queue.poll(); //删除并返回队头被删除的那个元素
                int remain_x = state[0];    //获取新状态
                int remain_y = state[1];
                if (remain_x == z || remain_y == z || remain_x + remain_y == z) {
                    return true;
                }

                Queue.add(new int[]{x, remain_y}); // 把 X 壶灌满
                Queue.add(new int[]{remain_x, y}); // 把 Y 壶灌满
                Queue.add(new int[]{0, remain_y}); // 把 X 壶倒空
                Queue.add(new int[]{remain_x, 0}); // 把 Y 壶倒空

                Queue.add(new int[]{remain_x - Math.min(remain_x, y - remain_y), remain_y + Math.min(remain_x, y - remain_y)});
                // 把 X 壶的水灌进 Y 壶，直至灌满或倒空
                Queue.add(new int[]{remain_x + Math.min(remain_y, x - remain_x), remain_y - Math.min(remain_y, x - remain_x)});
            }  // 把 Y 壶的水灌进 X 壶，直至灌满或倒空。
            return false;
        }

        public long hash(int[] state) {return  state[0] * 1000001L + state[1];
        }
    }
}

其实倒水问题用数学方法更快。

import java.util.Scanner;
public class newText2 {
    public static void main(String[] args) {
        Scanner mc = new Scanner(System.in);
        int x = mc.nextInt(); //分别输入两个瓶子的容积
        int y = mc.nextInt();
        int z = mc.nextInt();
        Solution sou = new Solution();
        System.out.println(sou.canMeasureWater(x, y, z));

    }

    static class Solution {
        public boolean canMeasureWater(int x, int y, int z) {
            if (z == 0) return true;
            if (z > (x + y)) return false;
            int a = Math.min(x, y);
            int b = Math.max(x, y);

            boolean[] record = new boolean[b];

            int remain = 0;
            while (!record[remain]) {
                record[remain] = true; //标记状态
                remain = (remain + a) % b;
                if (remain == z || remain + b == z) return true;
            }
            return false;
        }
    }
}

1.2最短路径问题

2.1迷宫问题：

返回最短路径的 步数

在N*M的迷宫中，计算并 输出S到G的最短路径
‘#’，’.’， ‘S’， 'G’分别表示墙壁、通道、起点、终点

解题思路：键入n,m,和迷宫；记录S和G的位置；DBS广搜，创建两个一维数组记录起点和终点位置，用 d[][] 标记走过路径；具体操作请看代码。

java.lang.*;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class newText2 {
    public static void main(String[] args) {
 Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();//行数
        int m = sc.nextInt();//列数
        String t = sc.nextLine();
        char[][] map = new char[n][m];
        int[] begin = new int[2]; //起点位置
        int[] end = new int[2];  //终点位置

        for (int i = 0; i < n; i++) { //按行输入字符,共输入n行,每输入一行，就依次判断是否 起点或终点
            String s = sc.nextLine();
            map[i] = s.toCharArray();
            if (s.contains("S")) {  // 当字符串 s 包含 " " 内指定的 char值时，方法返回true
                begin[0] = i;  //记录起点“s"所在行数，  下一行代码记录起点“s"所在列数
                begin[1] = s.indexOf("S");//查找指定字符"s"在其字符串中的下标。若"s"存在则返回所在字符串下标；不在则返回-1.
            }
            if (s.contains("G")) {
                end[0] = i;   //记录终点”G“所在 行数列数
                end[1] = s.indexOf("G");
            }
        }
        Solution put=new Solution();
        System.out.println( put.bfs(map, begin, end));
    }

    public static class Solution {
        public int bfs(char[][] map, int[] begin, int[] end) {
            int[] dx = {1, 0, -1, 0};//移动的四个方向
            int[] dy = {0, 1, 0, -1};
            int[][] d = new int[map.length][map[0].length];// 记录 到终点最短路径数的二维数组

            Queue<int[]> que = new LinkedList<int[]>();  //储存将要进行处理的点
            for (int i = 0; i < d.length; i++) {  //将所有的位置都初始化为最大
                for (int j = 0; j < d[0].length; j++) {
                    d[i][j] = Integer.MAX_VALUE; //Integer.MAX_VALUE 是整型可以支持的最大数
                }
            }
            que.offer(begin);//将起始点放入队列
            d[begin[0]][begin[1]] = 0;//将起始点最短路径设为0
            while (!que.isEmpty()) {// 队列非空时，执行循环
                int[] current = que.poll(); //取出队列中最前端的点
                if (current[0] == end[0] && current[1] == end[1])  break;//如果是终点则结束,最短路径为0
                for (int i = 0; i < 4; i++) {//四个方向循环

                    int ny = current[0] + dy[i];
                    int nx = current[1] + dx[i];
                    //判断是否可以走
                    if (ny >= 0 && ny < d.length && nx >= 0 && nx < d[0].length && map[ny][nx] != '#' && d[ny][nx] == Integer.MAX_VALUE) {

                        d[ny][nx] = d[current[0]][current[1]] + 1;//如果可以走，则将该点的距离加1
                        int[] c = {ny, nx};//将该点放入队列等待下次处理
                        que.offer(c);
                    }
                }
            }
            return d[end[0]][end[1]];
        }
    }
}

.

2.2还原路径

返回最短路径的步数和 路径

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
Input
一个n × m的二维数组，表示一个迷宫。数据保证有唯一解。
Output
左上角到右下角的最短路径，格式如样例所示。

Sample Input
 5 5
 0 1 0 0 0
 0 1 0 1 0
 0 0 0 0 0
 0 1 1 1 0
 0 0 0 1 0
 Sample Output
 8
 (0, 0)
 (1, 0)
 (2, 0)
 (2, 1)
 (2, 2)
 (2, 3)
 (2, 4)
 (3, 4)
 (4, 4)

解题思路:
是bfs+路径还原， 创建boolean 类 二维数组 visit[][] 标记走过路径, 通过广度优先搜索从起点进队，直至终点。搜索时，按照字典序搜索，将每步走的路径都封装入坐标类中保存，当搜索到终点时，直接输出保存的路径。

import java.lang.*;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class newText1 {
    public static void main(String[] args) {
        for (int i = 0; i < n; i++) { //输入迷宫
            String s = sc.next();
            for (int j = 0; j < m; j++) {
                map[i][j] = s.charAt(j) - '0'; //string类型转换为int类型的二维数组
            }
        }
        bfs(new Point(0, 0), n, m);
    }

    public static int dir[][] = new int[][]{{1, 0}, {0, -1}, {0, 1}, {-1, 0}}; //四个移动方向  对应下 左 右 上
    static Scanner sc = new Scanner(System.in);
    static int n = sc.nextInt(); //行数
    static int m = sc.nextInt(); //列数
    public static int[][] map = new int[n][m]; //储存迷宫
    public static boolean[][] visit = new boolean[n][m]; //标记走过路径，默认值为false

    public static void bfs(Point start, int n, int m) {
        Queue<Point> q = new LinkedList<Point>();
        q.add(start);
        visit[start.i][start.j] = true; // 标记起点
        while (!q.isEmpty()) {
            Point p = q.peek(); // 返回队列的头元素

            if (p.i == n - 1 && p.j == m - 1) { // 移动至终点时输出
                System.out.println(p.step);
                System.out.println(p.record);
                return;
            }

            for (int i = 0; i < 4; i++) {    //四个方向按'D', 'L', 'R', 'U'即对应 下 左 右 上 ，尝试移动
                int new_i = p.i + dir[i][0];
                int new_j = p.j + dir[i][1];
                Point temp = new Point(new_i, new_j);

                if (new_i >= 0 && new_j >= 0 && new_i < n && new_j < m && !visit[new_i][new_j] && map[new_i][new_j] != 1) {
                    visit[new_i][new_j] = true;
                    String y = String.valueOf(new_i); //将基本数据型（int）转换成字符串
                    String x = String.valueOf(new_j);
                    temp.step = p.step + 1;
                    temp.record = p.record + "(" + y + "," + x + ")" + "\n";
                    q.add(temp); //封装入坐标类
                }
            }
            q.poll(); //获取并删除队列中的第一个元素,获取新的new_i, new_j继续判断
        }
    }
}

class Point {
    int i;
    int j;
    int step; //走过步数
    String record; //路径

    public Point(int i, int j) {
        this.i = i;
        this.j = j;
        step = 0;
        record = "";
    }
}