
链表中的递归性质
前言
在前面的 链表的数据结构的实现 中,已经对链表数据结构的实现过程有了充分的了解了。但是对于链表而言,其实它还和递归相关联。虽然一般来说递归在树的数据结构中使用较多,因为在树这个结构中使用递归是非常方便的。在链表这个数据结构中也是可以使用递归的,因为链表本身具有天然的递归性质,只不过链表是一种线性结构,通常使用非递归的方式也可以很容易地实现它,所以大多数情况下都是使用循环的方式来实现链表。不过如果在链表中使用递归,可以帮助打好递归的基础以在后面可以更加深入地理解树这种数据结构和一些递归算法,这是非常具有好处的。所以在这里可以借助 LeetCode 上的一道关于链表的问题,使用递归的方式去解决它,以此达到理解链表中的递归性质的目的。
LeetCode 上关于链表的一道问题
203 考题目 移除链表中的元素
题目描述:
删除链表中等于给定值 val 的所有节点。示例:输入: 1->2->6->3->4->5->6, val = 6输出: 1->2->3->4->5来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/remove-linked-list-elements著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。题目提供的链表结点类:
/** * Definition for singly-linked list. */public class ListNode { int val; ListNode next; ListNode(int x) { val = x; }}题目提供的解题模板:
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */class Solution { public ListNode removeElements(ListNode head, int val) { }}-对于此题,可以先尝试使用非递归的方式然后使用虚拟头节点和不使用虚拟头节点分别实现来回顾一下链表的删除逻辑。
非递归方式及不使用虚拟头节点题解思路:
- 如果不使用虚拟头结点,那么首先可以直接判断 head 是否不为 null 以及它的值是否是要删除的元素,如果是则删除当前头节点。此处需要注意的是,很可能会存在多个要删除的元素都堆在链表头部或者整个链表都是要删除的元素,所以这里可以使用 while 循环来判断依次删除链表的当前头节点。
- 处理完头部部分后,就处理中间部分需要删除的元素,此时回顾一下链表的删除逻辑,需要先找到待删除节点的前置节点,所以以链表此时的头节点 head 开始,将其作为第一个前置节点 prev(因为此时头部已经处理完毕,没有要删除的元素了)。再通过 while 循环依次判断 prev 的下一个节点是否需要删除直到删除完所有要删除的元素为止。
- 最后返回头节点 head 即可,此时通过 head 可以获得删除元素后的链表。
以上思路实现为代码如下:
public class Solution { public ListNode removeElements(ListNode head, int val) { // 非递归不使用虚拟头结点的解决方案 // 把链表开始部分需要删除的元素删除 while (head != null && head.val == val) { ListNode delNode = head; head = head.next; delNode.next = null; } // 如果此时 head == null,说明链表中所有元素都需要删除,此时返回 head 或 null if (head == null) { return null; } // 处理链表中间需要删除的元素 ListNode prev = head; // 每次看 prev 的下一个元素是否需要被删除 while (prev.next != null) { if (prev.next.val == val) { ListNode delNode = prev.next; prev.next = delNode.next; delNode.next = null; } else { prev = prev.next; } } return head; }}提交结果:

接下来就使用虚拟头结点的方式来实现此题,思路如下:
- 创建一个虚拟头节点,并指向链表的头节点 head。
- 此时整个链表的所有元素都有一个前置节点,就可以统一使用通过前置节点的方式来删除待删除元素,此时以虚拟头节点开始,将其作为第一个前置节点 prev。再通过 while 循环依次判断 prev 的下一个节点是否需要删除直到删除完所有要删除的元素为止。
- 最后返回虚拟头节点的下一个节点即可,即返回 head。
以上思路实现为代码如下:
public class Solution { public ListNode removeElements(ListNode head, int val) { // 非递归使用虚拟头结点的解决方案 // 创建虚拟头节点 ListNode dummyHead = new ListNode(-999); dummyHead.next = head; // 处理链表中需要删除的元素 ListNode prev = dummyHead; // 每次看 prev 的下一个元素是否需要被删除 while (prev.next != null) { if (prev.next.val == val) { ListNode delNode = prev.next; prev.next = delNode.next; delNode.next = null; } else { prev = prev.next; } } // 返回链表头节点 return dummyHead.next; }}提交结果:

此时,两种方案都正确的运行了。对于链表的删除逻辑在使用虚拟头节点和不使用虚拟头节点的情况都实现了一遍,这也是在之前的链表的数据结构的实现中涉及到的部分,这里再次回顾一遍加深印象,也方便后面使用递归方式实现该题目后对比两种不同方式的异同。
递归的基本概念与示例
对于递归,本质上,就是将原来的问题,转化为更小的同一问题,直到转化为基本问题并解决基本问题后,再一步步的将结果返回达到求解原问题的目的。
举个例子:数组求和。

从图中可以看出,其实递归也就是将原问题的规模一步步地缩小,一直缩小到基本问题出现然后解出基本问题的解再往上依次返回根据这个基本解依次求出各个规模的解直到求出原问题的解。
以上过程编码实现如下:
/** * 数组求和递归示例 * * @author 踏雪彡寻梅 * @date 2020/2/8 - 10:30 */public class Sum { /** * 对 array 求和 * * @param array 求和的数组 * @return 返回求和结果 */ public static int sum(int[] array) { // 计算 array[0...n) 区间内所有数字的和 return sum(array, 0); } /** * 计算 array[l...n) 这个区间内所有数字的和 * * @param array 求和的数组 * @param l 左边界 * @return 返回求和的结果 */ private static int sum(int[] array, int l) { // 基本问题: 数组为空时返回 0 if (l == array.length) { return 0; } // 把原问题转换为小问题解决 return array[l] + sum(array, l + 1); } /** * 测试数组求和 */ public static void main(String[] args) { int[] nums = {1, 2, 3, 4, 5, 6, 7, 8}; System.out.println(sum(nums)); }}运行结果:

对于以上例子,可以这样理解:在使用递归时,可以注意递归函数的“宏观”语意。在上面的例子中,“宏观”语意就是计算 array[l...n) 区间内所有数字的和。这样子理解递归函数再去观看函数中的将原问题转换成小问题时,会更好地理解这个函数要做的事情,简单来说递归函数就是一个完成一个功能的函数,只不过是自己调用自己,每一次转换成小问题时完成的功能都是数组的某个数加上剩余数的和,直到无数可加为止。这个数组求和的递归过程如下图所示:
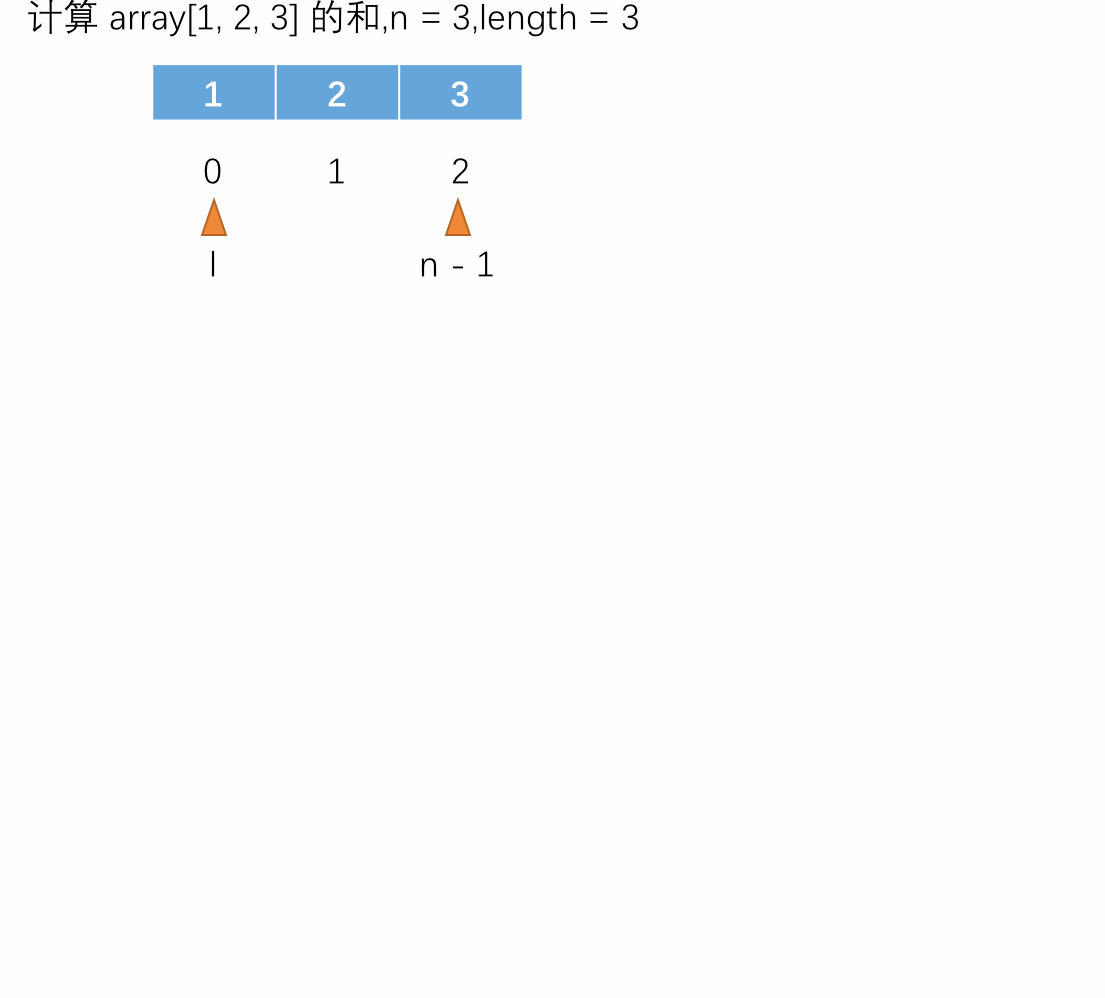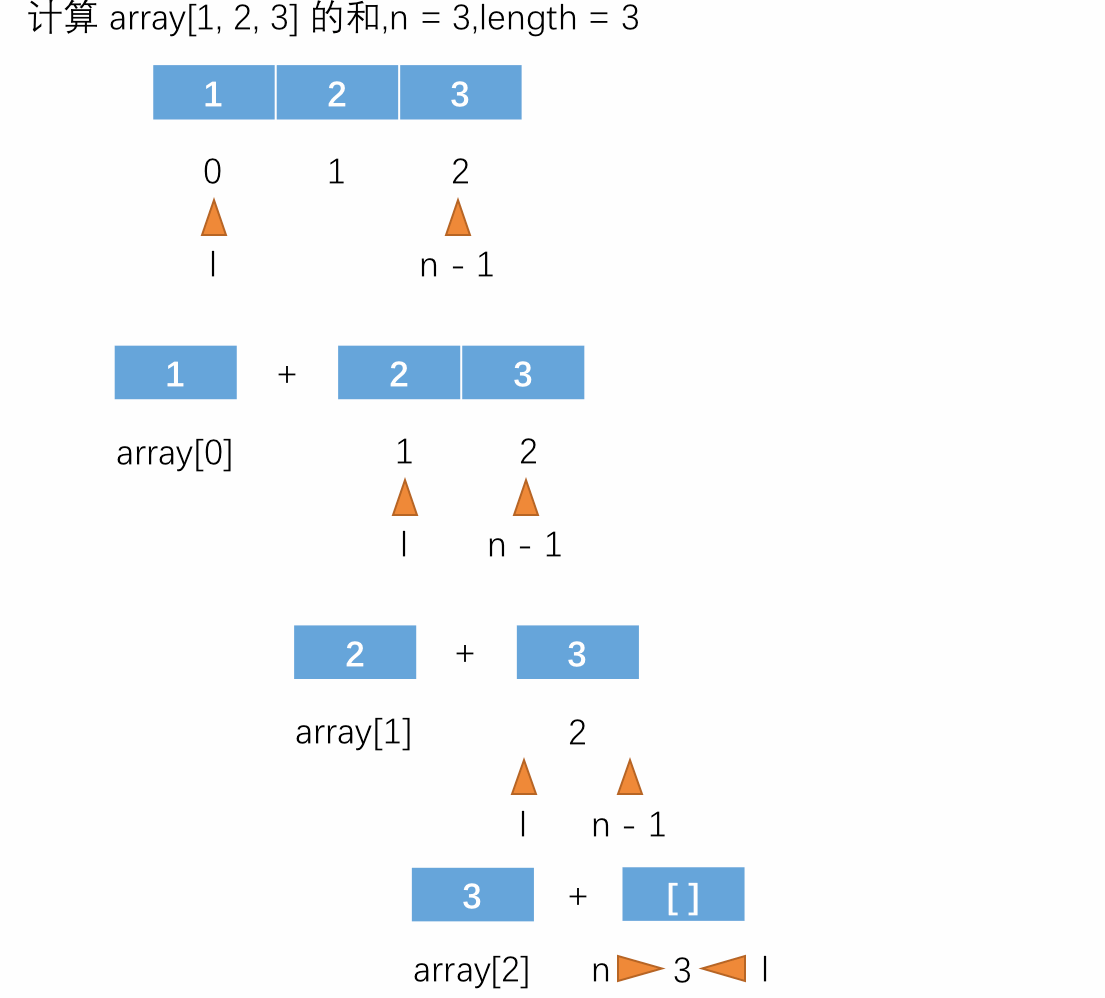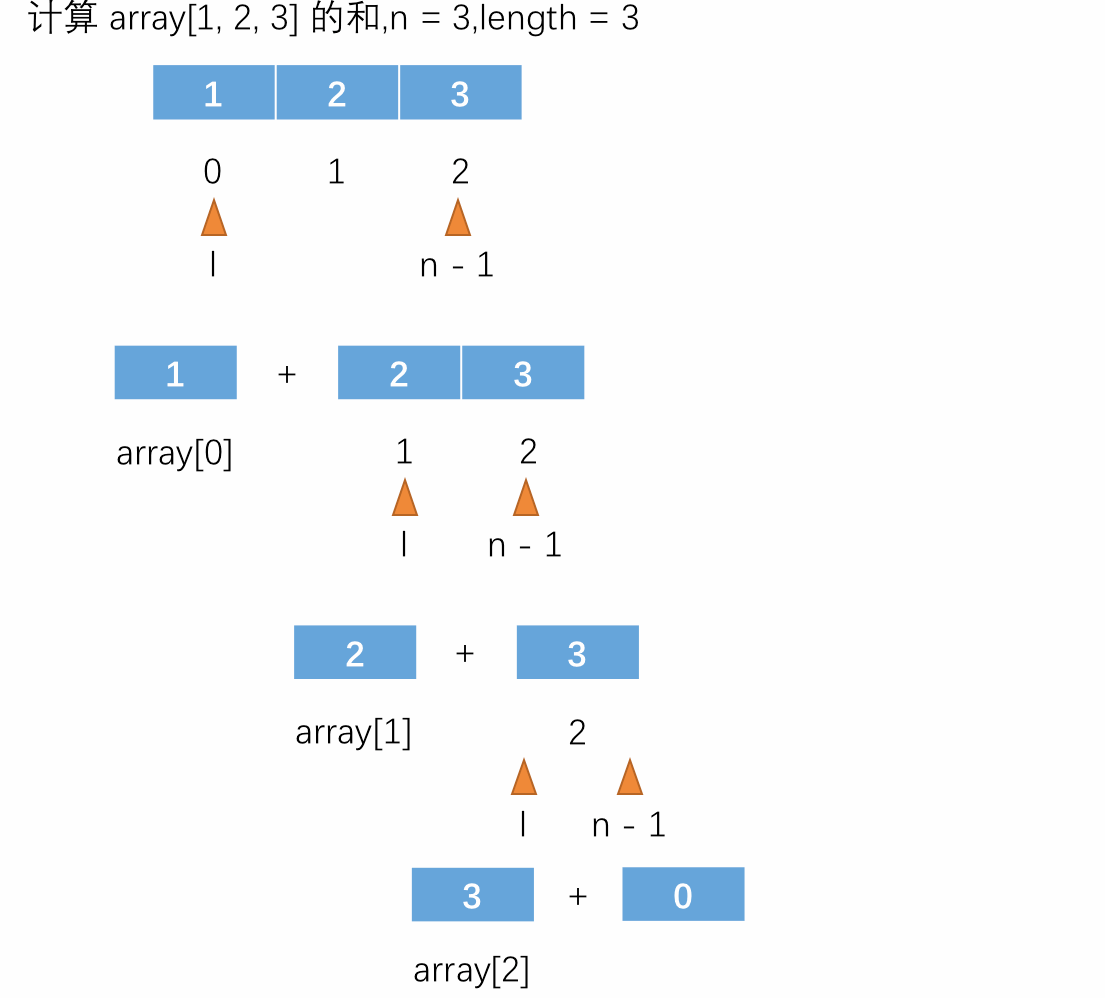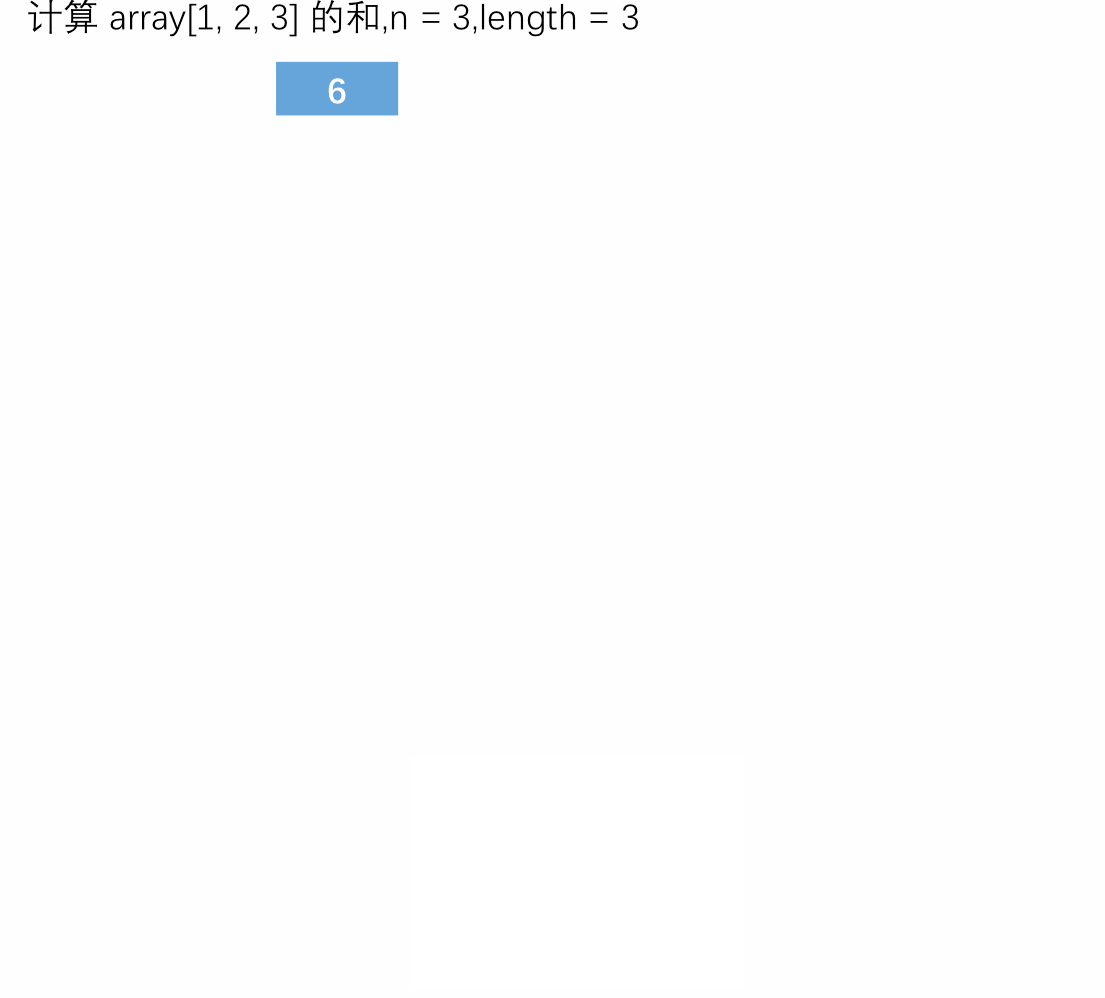
也可以使用下图表示,下图中的代码是进行拆分后的代码,为了更方便地展示过程:

至此,已经大致了解了递归的基本概念和基本流程了,接下来就看看链表所具有的天然的递归性质。
链表天然的递归性
对于链表而言,本质上就是将一个个节点挂接起来组成的。也就是下图的这个样子:

而其实对于链表,也可以应用递归理解成是由一个头节点后面挂接着一个更短的链表组成的。也就是下图的这个样子:

对于上图中的一个更短的链表,其中也是由一个头节点挂接着一个更短的链表形成的,依次类推,直到最后为 NULL 时,NULL 其实也就是一个链表了,此时就是递归方式的链表的基本问题。
所以此时再看回之前的 203 考题目:移除链表中的元素。就可以将题目提供的链表看成上图所示的结构,然后使用递归解决更小的链表中要删除的元素得到这个小问题的解,之后再看头节点是否需要删除,如果要删除就返回小问题的解,此时也就是原问题的解了;不删除的话就将头节点和小问题的解组合起来返回回去得到原问题的解。这个过程用图来表示为以下图示:

用代码实现后如下所示:
public class Solution { public ListNode removeElements(ListNode head, int val) { // 使用递归解决链表中移除元素 // 构建基本问题,链表为空时返回 null if (head == null) { return null; } // 构建小问题: 得到头节点后挂接着的更小的链表的解 ListNode result = removeElements(head.next, val); // 判断头节点是否需要删除,和小问题的解组合得到原问题的解 if (head.val == val) { // 头节点需要删除 return result; } else { // 头节点不需要删除,和小问题的解组合得到原问题的解 head.next = result; return head; } }}提交结果:

从提交结果可以验证实现的逻辑是没有错误的。此时代码还可以进行简化如下:
public class Solution { public ListNode removeElements(ListNode head, int val) { // 使用递归解决链表中移除元素 // 构建基本问题,链表为空时返回 null if (head == null) { return null; } // 构建小问题: 得到头节点后挂接着的更小的链表的解,然后挂接在头节点后面 head.next = removeElements(head.next, val); // 判断头节点是否需要删除,和小问题的解组合得到原问题的解 return head.val == val ? head.next : head; }}提交结果:

此时对比前面的非递归方式实现的题解,可以发现使用递归方式实现是非常优雅的,代码十分简洁易读。接下来就分析一下该递归运行的机制。递归运行过程如下图所示:
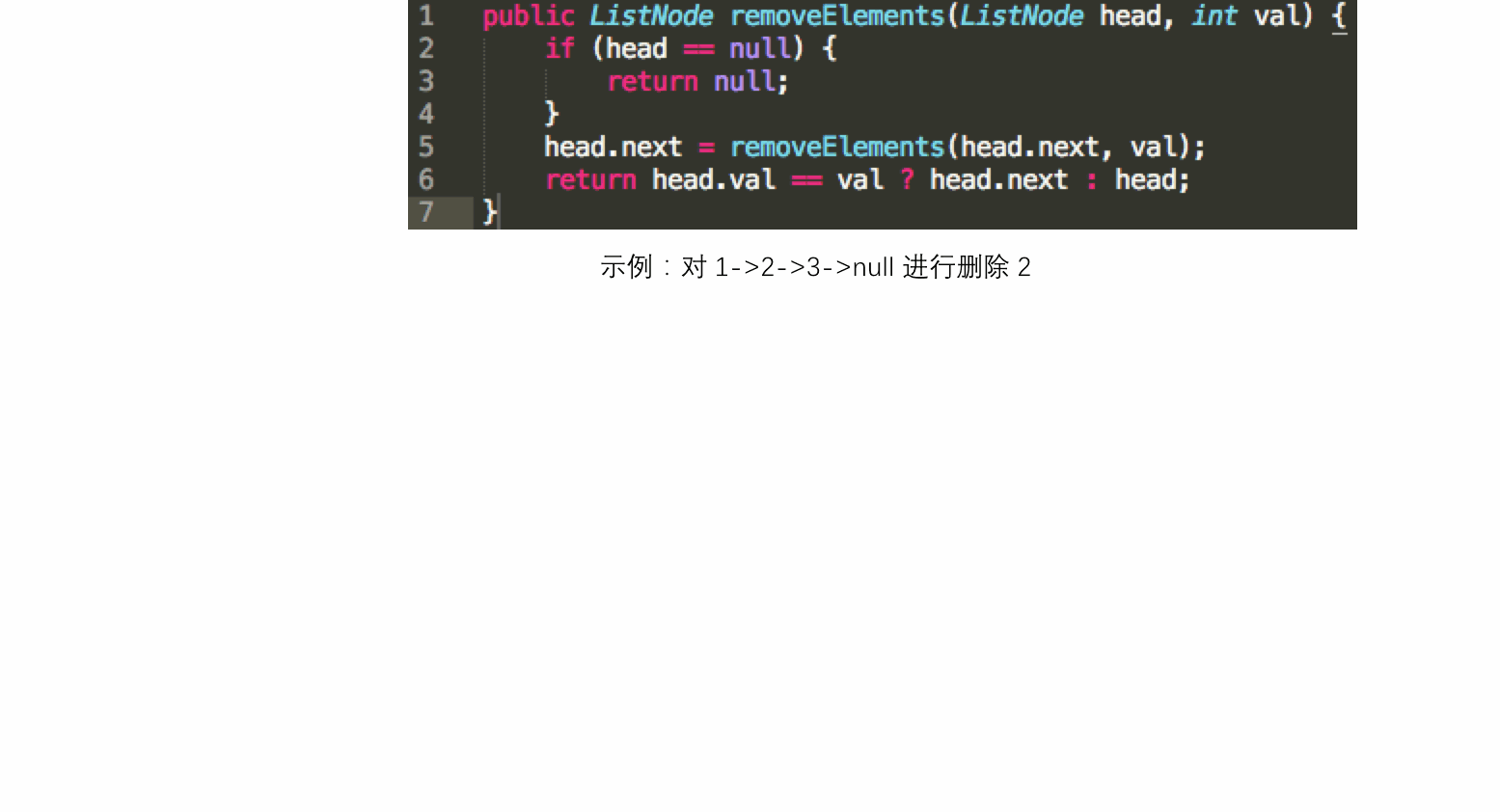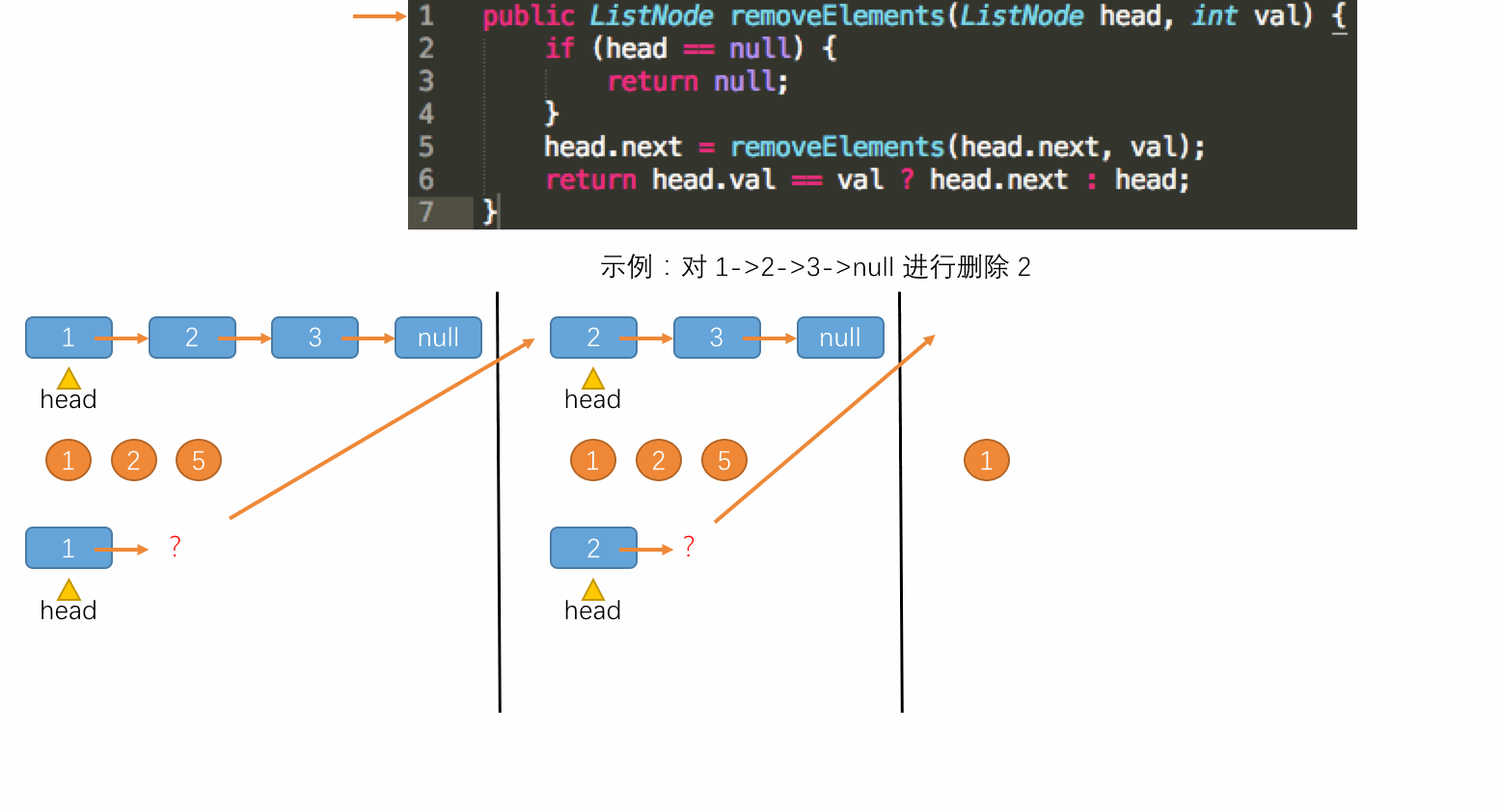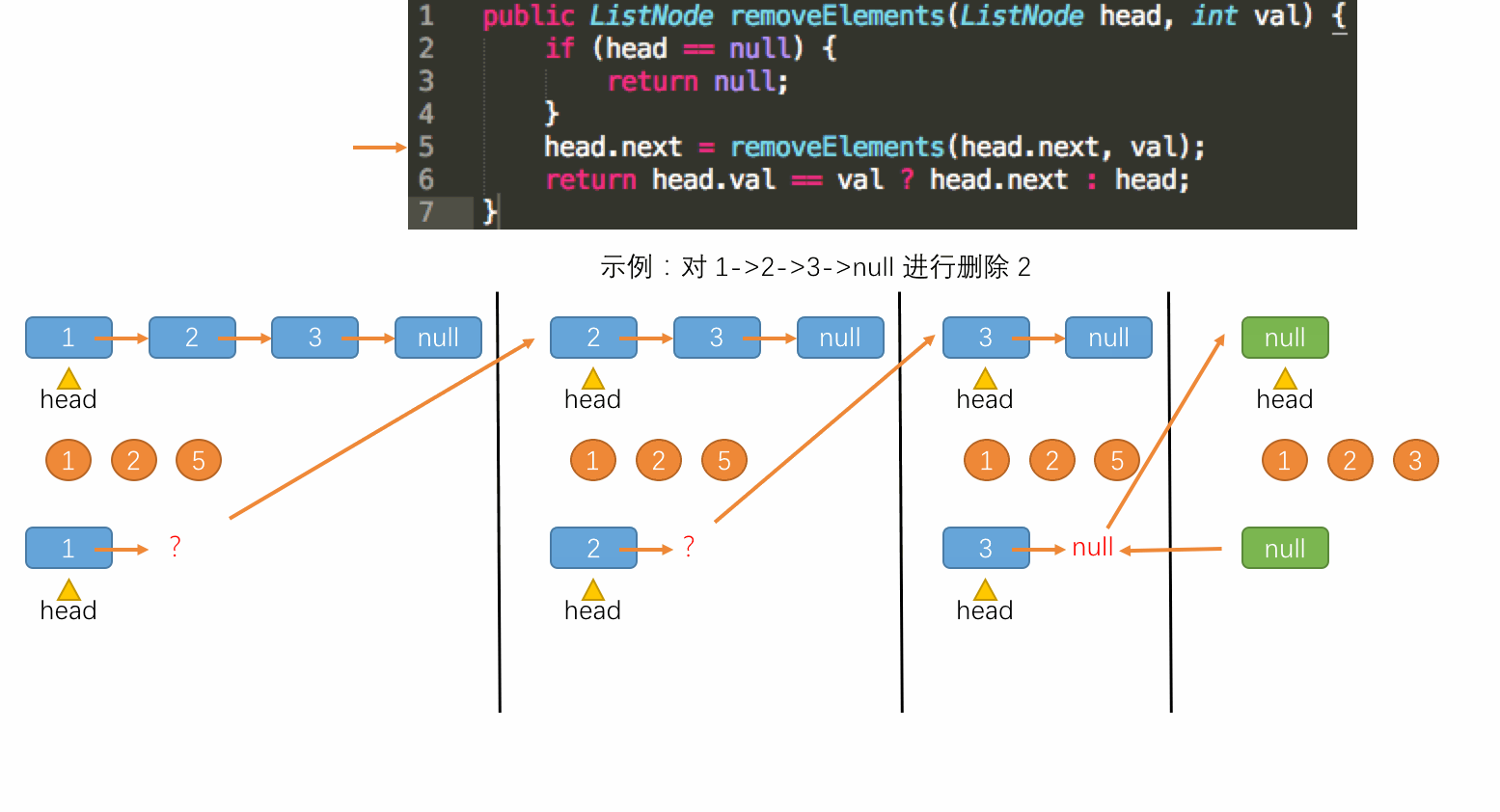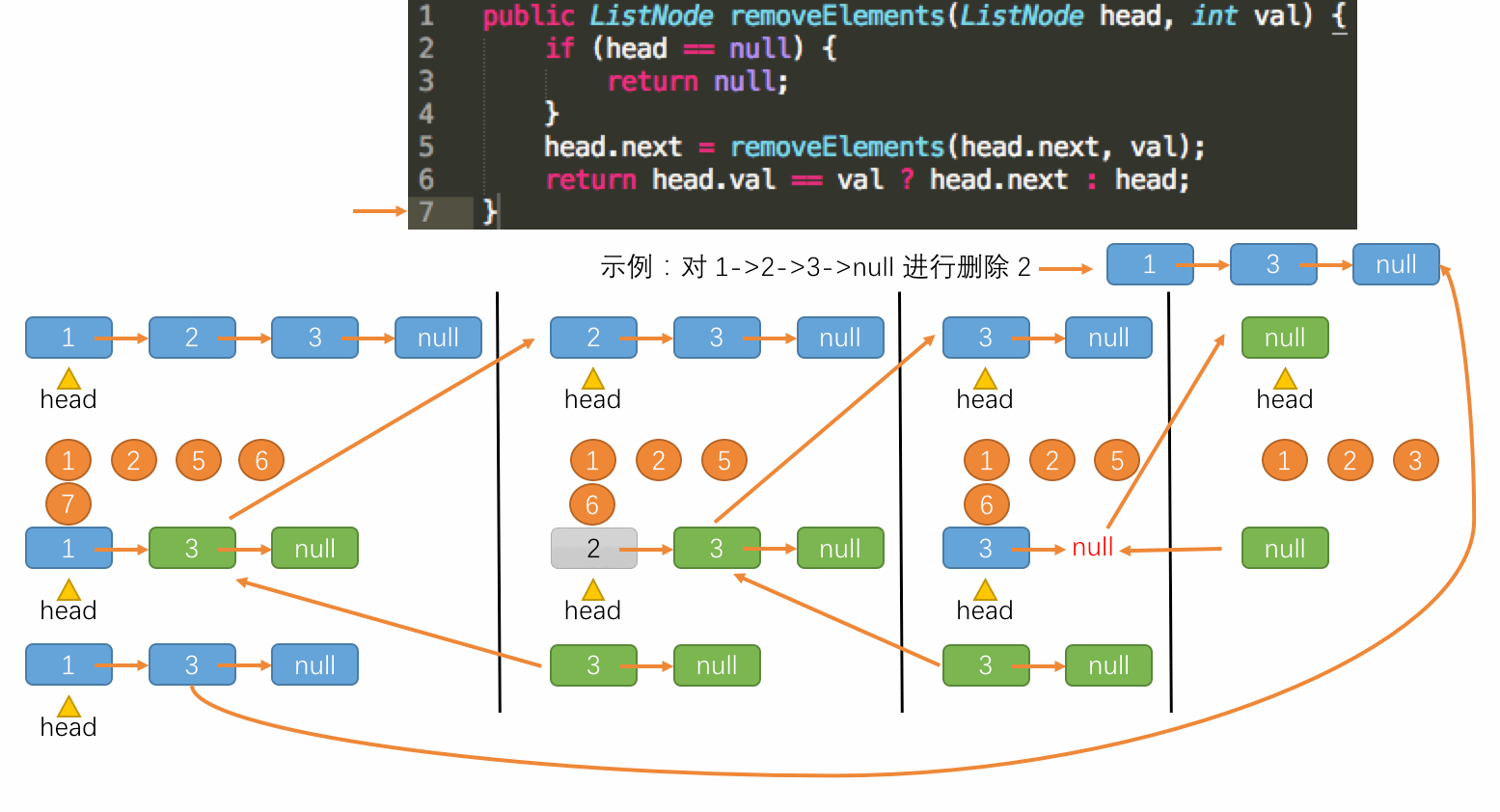
至此,这个题目的递归流程就走完了,对于以上过程,就是子过程的一步步调用,调用完毕之后,子过程计算出结果,再一步步地返回结果给上层调用,最终得到了结果。节点的删除发生在第 6 行语句上,这行语句也就是解决了更小规模的问题后得到解后组织当前调用构成了当前问题的解。
与此同时,需要注意的是递归调用是有代价的,代价则是函数的调用和使用系统占空间这两方面。在函数调用时是需要一些时间开销的,其中包括需要记录当前函数执行到哪个位置、函数中的局部变量是处于怎样的等等,然后将这个状态给压入系统占。然后在递归调用的过程中,是需要消耗系统栈的空间的,所以对于递归函数,如果不处理基本问题的话,递归函数将一直执行下去,直到将系统栈的空间使用完。同时如果使用递归处理数据量巨大的情况的时候,也有可能会使用完系统栈空间,比如上面的数组求和如果求和百万级别、千万级别的数据系统栈空间是不够用的,在链表中删除元素也是如此,如果链表过长系统栈空间也是不够用的。所以在这一点需要有所注意。
总而言之,使用递归来书写程序逻辑其实是比较简单的,这个特点在非线性结构中,比如树、图这些数据结构,这个特点会体现地十分明显。
小结
此时,对于递归和链表中的递归性质在使用了一个数组求和的例子和 LeetCode 上的一道题目的例子做了相应的过程分析之后已经有了充分的了解,也发现了使用递归来书写逻辑是非常简单易读的,相比之前使用非递归方式实现的题解其中的代码,递归方式的代码只有短短几行。但是相对应的,递归也是有一定的局限性的,在使用的过程中需要注意系统栈空间的占有,如果数据量太大很可能会撑爆系统栈空间,所以这一方面需要额外注意。





















