无迹卡尔曼滤波python 无迹卡尔曼滤波代码

无迹卡尔曼滤波不同于扩展卡尔曼滤波，它是概率密度分布的近似，由于没有将高阶项忽略，所以在求解非线性时精度较高。

UT变换的核心思想：近似一种概率分布比近似任意一个非线性函数或非线性变换要容易。

原理：

假设n维随机向量x:N(x均值，Px)，x通过非线性函数y=f(x)变换后得到n维的随机变量y。通过UT变换可以比较高的精度和较低的计算复杂度求得y的均值和方差Px。

UT的具体过程如下：

（1）计算2n+1个Sigma点及其权值：

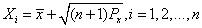
  根号下为矩阵平方根的第i列

 

 

 

 

  

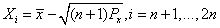
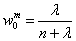
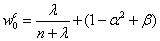
  依次为均值、方差的权值

 

 式中：

 

 α决定Sigma点的散步程度，通常取一小的正值；k通常取0；β用来描述x的分布信息，高斯情况下，β的最优值为2。

（2）计算Sigma点通过非线性函数f()的结果：

 

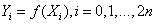
从而得知

 

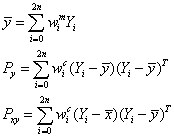
由于x的均值和方差都精确到二阶，计算得到y的均值和方差也精确到二阶，比线性化模型精度更高。