聚类算法阈值分割基于python 聚类算法选择

转载

autohost 2023-07-03 14:29:10

文章标签 聚类算法阈值分割基于python 数据分析聚类邻域迭代 文章分类 Python 后端开发

1. k近邻（knn）

1.1 步骤：

1.随机选择k个样本作为初始均值向量；
2.计算样本到各均值向量的距离，把它划到距离最小的簇；
3.计算新的均值向量；
4.迭代，直至均值向量未更新或到达最大次数。

优点：

原理比较简单，实现也是很容易;
算法的可解释度比较强；
调参方便，参数仅仅是簇数k。

缺点：

聚类中心的个数K 需要事先给定,交叉验证；
数据不平衡，或者非凸数据聚类效果差；
对噪音和异常点比较的敏感。

1.2 k如何选择

方法1： k-means++, 轮盘法选择距离较远的点
方法2：选用层次聚类进行出初始聚类，然后从k个类别中分别随机选取k个点。

1.3 大数据情形

mini batch k-means

聚类算法阈值分割基于python 聚类算法选择_数据分析

1.4 knn和k-Means

聚类算法阈值分割基于python 聚类算法选择_迭代_02

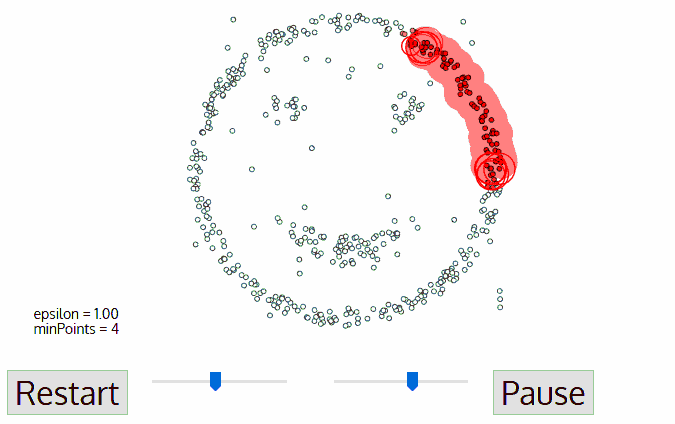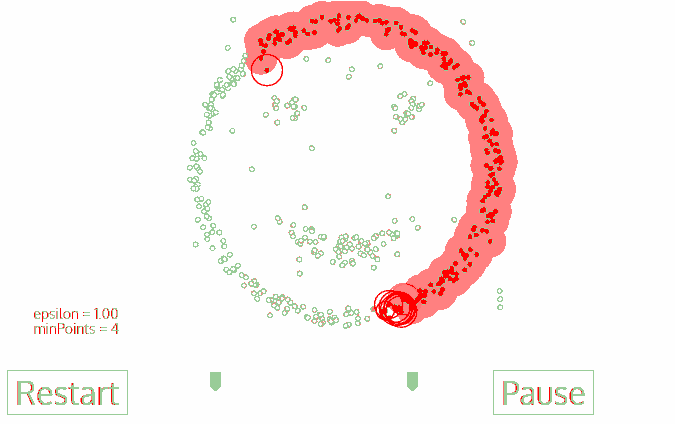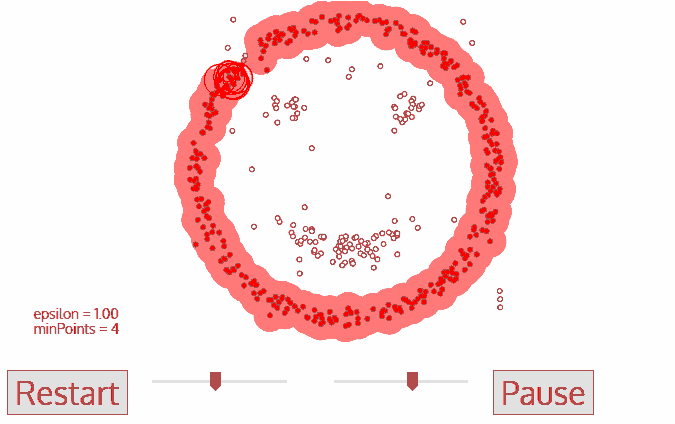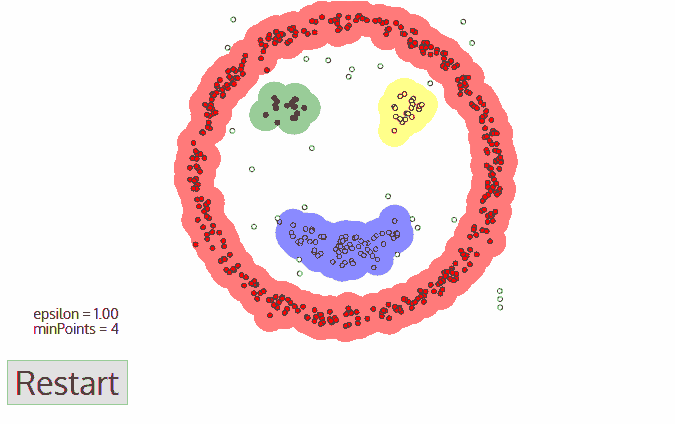
2. DBSCAN

步骤：

1、找到任意一个核心点，对该核心点进行扩充；
2、扩充方法是寻找从该核心点出发的所有密度相连的数据点；
3、遍历该核心的邻域内所有核心点，寻找与这些数据点密度相连的点。

相应概念：

-邻域：对于任意样本i和给定距离e，样本i的e邻域是指所有与样本i距离不大于e的样本集合；
-核心对象：若样本i的e邻域中至少包含MinPts个样本，则i是一个核心对象；
-密度直达：若样本j在样本i的e邻域中，且i是核心对象，则称样本j由样本i密度直达；
-密度可达：对于样本i和样本j，如果存在样本序列p1，p2，...，pn，其中p1=i，pn=j，并且pm由pm-1密度直达，则称样本i与样本j密度可达；
-密度相连：对于样本i和样本j，若存在样本k使得i与j均由k密度可达，则称i与j密度相连

优点：

不需要确定要划分的聚类个数；
抗噪声，在聚类的同时发现异常点，对数据集中的异常点不敏感；
处理任意形状和大小的簇，可以用于凸数据集。

缺点：

数据量大时内存消耗大，相比K-Means参数多一些；
样本集的密度不均匀、类间距很大时，聚类质量较差；

3. mean-shift均值飘移动

步骤：

在未被标记的数据点中随机选择一个点作为起始中心点center；
找出以center为中心半径为radius的区域中出现的所有数据点，认为这些点同属于一个聚类C。同时在该聚类中记录数据点出现的次数加1。
以center为中心点，计算从center开始到集合M中每个元素的向量，将这些向量相加，得到向量shift。
center = center + shift。即center沿着shift的方向移动，移动距离是||shift||。
重复步骤2、3、4，直到shift的很小（就是迭代到收敛），记住此时的center。注意，这个迭代过程中遇到的点都应该归类到簇C。
如果收敛时当前簇C的center与其它已经存在的簇C2中心的距离小于阈值，那么把C2和C合并，数据点出现次数也对应合并。否则，把C作为新的聚类。
重复1、2、3、4、5直到所有的点都被标记为已访问。
分类：根据每个类，对每个点的访问频率，取访问频率最大的那个类，作为当前点集的所属类。

Mean Shift方法适合概率密度函数有极值且在某一局部区域内唯一，即选择的特征数据点能够较为明显的判定目标，亦即显著特征点。显然此方法，Mean Shift的基本形式不适合等概率特征点，即特征点是均匀分布的情况。

4. 层次聚类

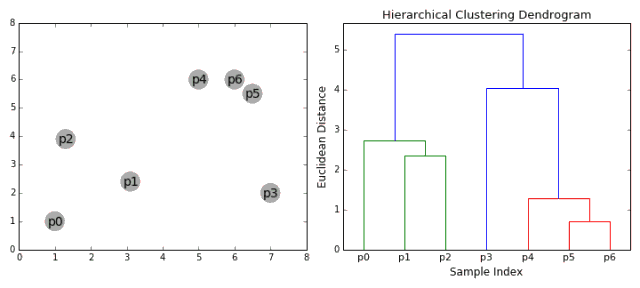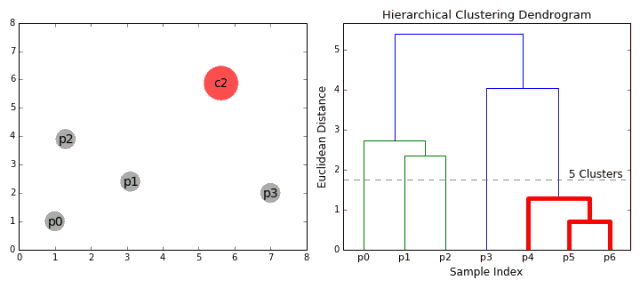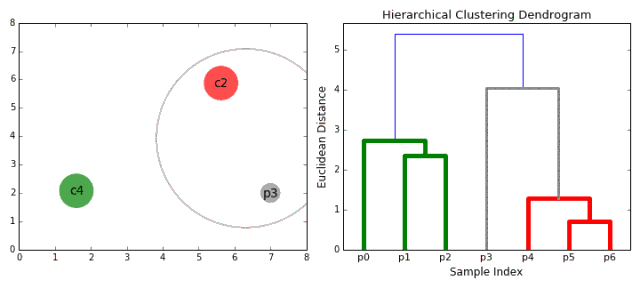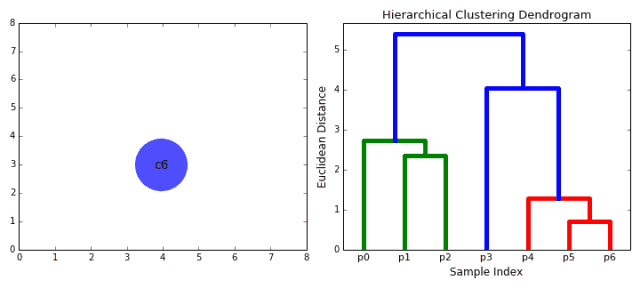
聚类算法阈值分割基于python 聚类算法选择_聚类_04

1.首先将每一个数据点看成一个类别，通过计算点与点之间的距离将距离近的点归为一个子类，作为下一次聚类的基础；
2.每一次迭代将两个元素聚类成一个，上述的子类中距离最近的两两又合并为新的子类。最相近的都被合并在一起；
3.重复步骤二直到所有的类别都合并为一个根节点。基于此我们可以选择我们需要聚类的数目，并根据树来进行选择。