写一个图的算法(二)
有权图的最小生成树Krusk算法
Kruskal算法计算有权无向图的最小生成树
测试用例:
8 16
4 5 .35
4 7 .37
5 7 .28
0 7 .16
1 5 .32
0 4 .38
2 3 .17
1 7 .19
0 2 .26
1 2 .36
1 3 .29
2 7 .34
6 2 .40
3 6 .52
6 0 .58
6 4 .93
import java.util.ArrayList;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Scanner;
public class KruskalMST {
//有权图
static List<List<Double[]>> totallist;
//最小生成树
static List<Double[]> minTree;
static int[] rank;
static int[] parent;
static double mstWeight;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int M = scanner.nextInt();
totallist = new ArrayList<>();
minTree = new ArrayList<>();
rank = new int[N];
parent = new int[N];
for(int i=0;i<N;i++) {
rank[i] = 1;
parent[i] = i;
totallist.add(new LinkedList<>());
}
//最小堆
PriorityQueue<Double[]> queue = new PriorityQueue<>(new Comparator<Double[]>() {
@Override
public int compare(Double[] o1, Double[] o2) {
// TODO Auto-generated method stub
return o1[2].compareTo(o2[2]);
}
});
for(int i=0;i<M;i++) {
int s = scanner.nextInt();
double ds = Double.valueOf(s);
int e = scanner.nextInt();
double de = Double.valueOf(e);
double w = scanner.nextDouble();
totallist.get(s).add(new Double[] {ds,de,w});
if(s!=e) {
totallist.get(e).add(new Double[] {de,ds,w});
}
queue.offer(new Double[] {ds,de,w});
/*if(s<e) { //s<=e
queue.offer(new Double[] {ds,de,w});
}*/
}
while(!queue.isEmpty()) {
// 从最小堆中依次从小到大取出所有的边
Double[] top = queue.poll();
int startIndex = top[0].intValue();
int toIndex = top[1].intValue();
// 如果该边的两个端点是联通的, 说明加入这条边将产生环, 扔掉这条边
if(isConnected(startIndex, toIndex)) {
continue;
}
// 否则, 将这条边添加进最小生成树, 同时标记边的两个端点联通
minTree.add(top);
unionElement(startIndex,toIndex);
}
mstWeight = minTree.get(0)[2];
for(int i=1;i<minTree.size();i++) {
mstWeight = mstWeight+minTree.get(i)[2];
}
System.out.println(mstWeight);
}
private static boolean isConnected(int v,int w) {
return find(v)==find(w);
}
private static int find(int v) {
// TODO Auto-generated method stub
while(v!=parent[v]) {
parent[v] = parent[parent[v]];
v = parent[v];
}
return v;
}
private static void unionElement(int v,int w) {
int vRoot = find(v);
int wRoot = find(w);
if(vRoot==wRoot) {
return;
}
if(rank[vRoot]<rank[wRoot]) {
parent[vRoot] = wRoot;
}else if(rank[wRoot]<rank[vRoot]) {
parent[wRoot] = vRoot;
}else {
parent[vRoot] =wRoot;
rank[wRoot]+=1;
}
}
}
输出:

Dijsktra与FloyId最短路径算法
单源最短路径问题解决了所有的顶点距离起始顶点(可以有不同的起始点)最小的路径问题,出发点是距离某一个起始顶点距离最小。单源的意思就是从一个起始点到其他可以抵达点的最短路径(广度优先就是求无向图的单源最短路径),并不仅仅局限于从一点到达另外一点的最短距离。
而Kruskal则计算的是最小生成树图(无向图)中所有的边权值总和是最小,出发点是整个图中的树中所有的点。
戴克斯特拉算法(Dijkstra's algorithm)是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。迪科斯彻算法使用了广度优先搜索解决非负权有向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
该算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合。每一个图中的边,都是两个顶点所形成的有序元素对。(u, v) 表示从顶点 u 到 v 有路径相连。我们以 E 表示G中所有边的集合,而边的权重则由权重函数 w: E → [0, ∞] 定义。因此,w(u, v) 就是从顶点 u 到顶点 v 的非负权重(weight)。边的权重可以想像成两个顶点之间的距离。任两点间路径的权重,就是该路径上所有边的权重总和。已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t的最低权重路径(例如,最短路径)。这个算法也可以在一个图中,找到从一个顶点 s 到任何其他顶点的最短路径。对于不含负权的有向图,Dijkstra算法是目前已知的最快的单源最短路径算法。
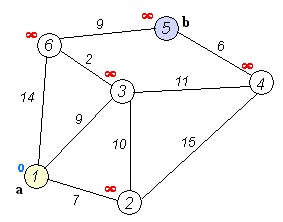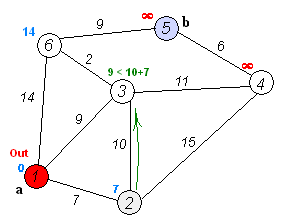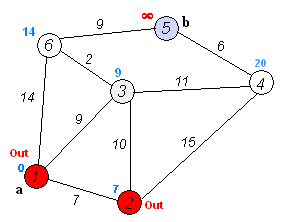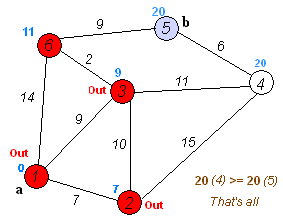
算法步骤:
1. 初始时令 S={V0},T={其余顶点},T中顶点对应的距离值
若存在<v0,vi>,d(V0,Vi)为<v0,vi>弧上的权值
若不存在<v0,vi>,d(V0,Vi)为∞
2. 从T中选取一个其距离值为最小的顶点W且不在S中,加入S
3. 对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值
重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止
测试用例:

5 8
0 1 5
0 2 2
0 3 6
1 4 1
2 1 1
2 4 5
2 3 3
3 4 2
通过PriorityQueue进行实现的,起始点为0,到达4最短的距离
import java.util.ArrayList;
import java.util.Comparator;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Scanner;
/*
* 4:40:54
*/
public class Dijkstra2 {
static List<List<int[]>> totallist;
static int[] distTO; //distTo[i]存储从起始点s到i的最短路径长度
static boolean[] visited;
static int[][] from; //from[i]记录最短路径中, 到达i点的边是哪一条,可以用来恢复整个最短路径
static int N;
static int start;
static final int _INTMAX_ = 2087654321;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
N = scanner.nextInt();
int M = scanner.nextInt();
totallist = new ArrayList<>();
for(int i=0;i<N;i++) {
totallist.add(new LinkedList<>());
}
for(int i=0;i<M;i++) {
int s = scanner.nextInt();
int e = scanner.nextInt();
int w = scanner.nextInt();
totallist.get(s).add(new int[] {s,e,w});
//无向图
//totallist.get(e).add(new int[] {e,s,w});
}
//
//如果没有目的地,要执行到最后dijkstra(start,-1);
start = 0;
int dest = -1;
dijkstra(start,dest);
int minRoute = distTO[4];
System.out.println(minRoute);
for(int i=1;i<N;i++) {
if(hasPathTo(i)) {
System.out.println("Shortest Path to " + i + " : " + showPathTo(i));
showPath(i);
}
}
}
private static void dijkstra(int start, int dest) {
// TODO Auto-generated method stub
distTO = new int[N];
visited = new boolean[N];
from = new int[N][3];
for(int i=0;i<N;i++) {
distTO[i] = _INTMAX_;
}
//最小堆
PriorityQueue<int[]> queue =new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
// TODO Auto-generated method stub
return o1[1]-o2[1];
}
});
distTO[start] = 0;
from[0]= new int[] {start,start,0}; //起始点到起始点的距离为0
queue.add(new int[] {start,0});
while(!queue.isEmpty()) { //找离起始点最短的边
int[] cur = queue.poll();
visited[cur[0]] = true;
if(cur[0]==dest) break; //找到终点
for(int[] item:totallist.get(cur[0])) {
if(!visited[item[1]]) {
int startIndex = item[0];
int toIndex = item[1];
int weight = item[2];
weight+=cur[1];
if(weight<distTO[toIndex]) {
distTO[toIndex] = weight;
from[toIndex] = item;
queue.add(new int[] {toIndex,weight});
}
}
/*if(!visited[toIndex]) {
if(from[toIndex].length==0||distTO[cur[0]]+weight<distTO[toIndex]) {
distTO[toIndex] = distTO[cur[0]]+weight;
from[toIndex] = new int[] {startIndex,toIndex,weight};
}
}*/
}
}
}
private static boolean hasPathTo(int w) {
return visited[w];
}
private static int showPathTo(int w) {
return distTO[w];
}
private static List<int[]> shortestPath(int w){
Deque<int[]> deque = new LinkedList<>();
int[] e = from[w];
while(e[0]!=start) {
deque.push(e);
e = from[e[0]];
}
deque.push(e);
List<int[]> res = new ArrayList<>();
while(!deque.isEmpty()) {
int[] retItem = deque.pop();
res.add(retItem);
}
return res;
}
private static void showPath(int w) {
List<int[]> path = shortestPath(w);
for(int i =0;i<path.size();i++) {
System.out.println(path.get(i)[0]+"->");
if(i==path.size()-1) {
System.out.println(path.get(i)[1]);
}
}
}
}
输出:

int start = 2; //其实点为2
int dest = -1; //走到头
dijkstra(start,dest);
int minRoute = distTO[4]; //终点4
System.out.println(minRoute);
输出:2
经典案例
从某一个点出发,按照顺序到达下一个指定的结点,不能提前先到达其他指定的节点,最后要返回起始点,计算经过最短的路径。
例如下面的测试用例,从7结点开始,先到1结点,然后到5结点,最后到7结点,请问经过最短的距离
7 12 2 7 //节点个数、节点间路径的个数、需要按顺序依次到达的节点、开始的节点
1 5
1 2
6 1
3 1
2 3
2 4
2 5
2 7
3 4
4 5
5 6
5 7
6 7
使用Dijkstra计算单源最短路径
public class Dijkstra {
static List<List<int[]>> totallist;
static int[] distTO; //distTo[i]存储从起始点s到i的最短路径长度
static boolean[] visited;
static int[][] from; //from[i]记录最短路径中, 到达i点的边是哪一条,可以用来恢复整个最短路径
static int N;
static final int _INTMAX_ = 2087654321;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
N = scanner.nextInt();
int M = scanner.nextInt();
int K = scanner.nextInt();
int S = scanner.nextInt();
totallist = new ArrayList<>();
int[] arr = new int[K+2];
for(int i=0;i<N;i++) {
totallist.add(new LinkedList<>());
}
arr[0] = S-1;
for(int i =0;i<K;i++) {
arr[i+1] = scanner.nextInt()-1;
}
arr[K+1] = S-1;
for(int i=0;i<M;i++) {
int s = scanner.nextInt();
int e = scanner.nextInt();
int w = 1;
totallist.get(s-1).add(new int[] {s-1,e-1,w});
totallist.get(e-1).add(new int[] {e-1,s-1,w});
}
int total = 0;
for(int i=0;i<arr.length-1;i++) {
int start = arr[i];
int dest = arr[i+1];
dijkstra(start,dest);
int minRoute = distTO[dest];
total+=minRoute;
}
System.out.println(total);
}
private static void dijkstra(int start, int dest) {
// TODO Auto-generated method stub
distTO = new int[N];
visited = new boolean[N];
from = new int[N][2];
for(int i=0;i<N;i++) {
distTO[i] = _INTMAX_;
}
//最小堆
PriorityQueue<int[]> queue =new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
// TODO Auto-generated method stub
return o1[1]-o2[1];
}
});
distTO[start] = 0;
from[0]= new int[] {start,start,0}; //起始点到起始点的距离为0
queue.add(new int[] {start,0});
while(!queue.isEmpty()) { //找离起始点最短的边
int[] cur = queue.poll();
visited[cur[0]] = true;
if(cur[0]==dest) break; //找到终点
for(int[] item:totallist.get(cur[0])) {
if(!visited[item[1]]) {
int startIndex = item[0];
int toIndex = item[1];
int weight = item[2];
weight+=cur[1];
if(weight<distTO[toIndex]) {
distTO[toIndex] = weight;
queue.add(new int[] {toIndex,weight});
}
}
/*if(!visited[toIndex]) {
if(from[toIndex].length==0||distTO[cur[0]]+weight<distTO[toIndex]) {
distTO[toIndex] = distTO[cur[0]]+weight;
from[toIndex] = new int[] {startIndex,toIndex,weight};
}
}*/
}
}
}
}输出:5
负权边Bellman-Ford最短路径算法
如果一个图中有负权环的时候,从一点到任何一点如果能通过负权环,那么便可以在负权环中不停的转下去,最短路径最后为负无穷,或者说没有最小路径。
Bellman-Ford算法使用的前提可以有负权边,单不能有负权环。
Bellman-Ford也可以帮助我们判断图中是否有负权环,如果没有负权环从一个点到另一个点的最短路径最多经过所有的V个顶点,有V-1条边,否则存在顶点经过了两次,既存在负权环。
Bellman-Ford算法其实对所有的点进行V-1次松弛操作,就找到了从原点到其他所有点的最短路径,如果还能继续松弛操作则图中有负权环。
案例:

测试用例
5 8
0 1 5
0 2 2
0 3 6
1 2 -4
1 4 2
2 4 5
2 3 3
4 3 -3
有负权环的
5 9
0 1 5
0 2 2
0 3 6
1 2 -4
2 1 1
1 4 2
2 4 5
2 3 3
4 3 -3
Bellman-Ford计算负权边单源最短路径
/*
* 5:38:03 5:38:15 5:38:38
*/
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
public class BellmanFord {
static List<List<int[]>> totallist;
static int start;
static int[] distTo;
static int[][] from;
static int N;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
N = scanner.nextInt();
int M = scanner.nextInt();
totallist = new ArrayList<>();
distTo = new int[N];
from = new int[N][3];
for(int i=0;i<N;i++) {
totallist.add(new LinkedList<>());
from[i] = null;
}
for(int i=0;i<M;i++) {
int s = scanner.nextInt();
int e = scanner.nextInt();
int w = scanner.nextInt();
totallist.get(s).add(new int[] {s,e,w});
}
// 设置distTo[start] = 0, 并且让from[start]不为空, 表示初始s节点可达且距离为0
int start = 0;
distTo[start] = 0;
from[start] = new int[] {start,start,0};
// Bellman-Ford的过程
// 进行V-1次循环, 每一次循环求出从起点到其余所有点, 最多使用pass步可到达的最短距离
for(int pass=1;pass<N;pass++) {
// 每次循环中对所有的边进行一遍松弛操作
// 遍历所有边的方式是先遍历所有的顶点, 然后遍历和所有顶点相邻的所有边
for(int k=0;k<N;k++) {
for(int[] item:totallist.get(k)) {
int startIndex = item[0];
int toIndex = item[1];
int weight = item[2];
// 对于每一个边首先判断e->v()可达
// 之后看如果e->w()以前没有到达过, 显然我们可以更新distTo[e->w()]
// 或者e->w()以前虽然到达过, 但是通过这个e我们可以获得一个更短的距离, 即可以进行一次松弛操作, 我们也可以更新distTo[e->w()]
if(from[startIndex]!= null&&(from[toIndex]== null||distTo[startIndex]+weight<distTo[toIndex])) {
distTo[toIndex] = distTo[startIndex]+weight;
from[toIndex] = item;
}
}
}
}
//判断是否有负权环
boolean hasNegativeCycle = detectNegativeCycle();
// 返回从s点到w点的最短路径长度
int end = 4;
int minRoute = distTo[end];
System.out.println(hasNegativeCycle+" "+minRoute);
for(int m=1;m<N;m++) {
System.out.println("Shortest Path to " + m + " : " + distTo[m]);
showPath(m);
}
}
// 判断图中是否有负权环
private static boolean detectNegativeCycle() {
// TODO Auto-generated method stub
for(int i =0;i<N;i++) {
for(int[] item:totallist.get(i)) {
if(from[item[0]].length>0&&distTo[item[0]]+item[2]<distTo[item[1]]) {
return true;
}
}
}
return false;
}
private static List<int[]> shortestPath(int w){
Deque<int[]> deque = new LinkedList<>();
int[] e = from[w];
while(e[0]!=start) {
deque.push(e);
e = from[e[0]];
}
deque.push(e);
List<int[]> res = new ArrayList<>();
while(!deque.isEmpty()) {
int[] retItem = deque.pop();
res.add(retItem);
}
return res;
}
private static void showPath(int w) {
List<int[]> path = shortestPath(w);
for(int i =0;i<path.size();i++) {
System.out.println(path.get(i)[0]+"->");
if(i==path.size()-1) {
System.out.println(path.get(i)[1]);
}
}
}
}
输出:






















