本文借鉴于:
http://blog.sina.com.cn/s/blog_76ed75bf0101hcor.html
循环冗余校验码(Cyclic Redundancy Check ,CRC)是一种检错、纠错能力很强的数据校验码,主要用于计算机网络、同步通信及磁表面存储器等应用场合。
循环冗余校验码是通过除法运算来建立有效信息位和校验位之间的约定关系。假定,待编码的有效信息以多项式M(X)表示,将它左移若干位后,用另一个约定的多项式G(X)去除,所产生的余数就是校验位。有效信息位与校验位相拼接就构成了CRC码。当接收方收到发来的CRC码后,他仍用约定的多项式G(X)去除,若余数为0,表明该代码接收无误;若余数不为0,表明某一位出错,再进一步由余数值确定出错的位置,并予以纠正。
循环冗余校验码的编码方法
循环冗余校验码由两部分组成,左边为信息位,右边为校验位。若信息位为N位,校验位为K位,则该校验码被称为(N+K,N)码。
这里, 需介绍一下模 2的运算规则。
模2运算不考虑加法的进位和减法的借位,即0±0=0,0±1=1,1±0=1,1±1=0。作模2除法时,上商的原则是当部分余数首位是1时(即使被除数比除数小),商取1,反之商取0,然后按模2加减求得余数。当被除数逐步除完时,最终的余数比除数少一位,此余数就是校验位。
算法原理
假设数据传输过程中需要发送15位的二进制信息g=101001110100001,这串二进制码可表示为代数多项式g(x) = x^14 + x^12 + x^9 + x^8 + x^7 + x^5 + 1,其中g中第k位的值,对应g(x)中x^k的系数。将g(x)乘以x^m,既将g后加m个0,然后除以m阶多项式h(x),得到的(m-1)阶余项r(x)对应的二进制码r就是CRC编码。
h(x)可以自由选择或者使用国际通行标准,一般按照h(x)的阶数m,将CRC算法称为CRC-m,比如CRC-32、CRC-64等。国际通行标准可以参看http://en.wikipedia.org/wiki/Cyclic_redundancy_check
g(x)和h(x)的除运算,可以通过g和h做xor(异或)运算。比如将11001与10101做xor运算:
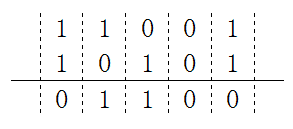
明白了xor运算法则后,举一个例子使用CRC-8算法求101001110100001的效验码。CRC-8标准的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1,既h是9位的二进制串111010101。

经过迭代运算后,最终得到的r是10001100,这就是CRC效验码。





















