线性回归在整个财务中广泛应用于众多应用程序中。在之前的教程中,我们使用普通最小二乘法(OLS)计算了公司的beta与相对索引的比较。现在,我们将使用线性回归来估计股票价格。
线性回归是一种用于模拟因变量(y)和自变量(x)之间关系的方法。通过简单的线性回归,只有一个自变量x。可能有许多独立变量属于多元线性回归的范畴。在这种情况下,我们只有一个自变量即日期。对于第一个日期上升到日期向量长度的整数,该日期将由1开始的整数表示,该日期可以根据时间序列数据而变化。当然,我们的因变量将是股票的价格。为了理解线性回归,您必须了解您可能在学校早期学到的相当基本的等式。
y = a + bx
- Y =预测值或因变量
- b =斜率
- x =系数或自变量
- a = 截距
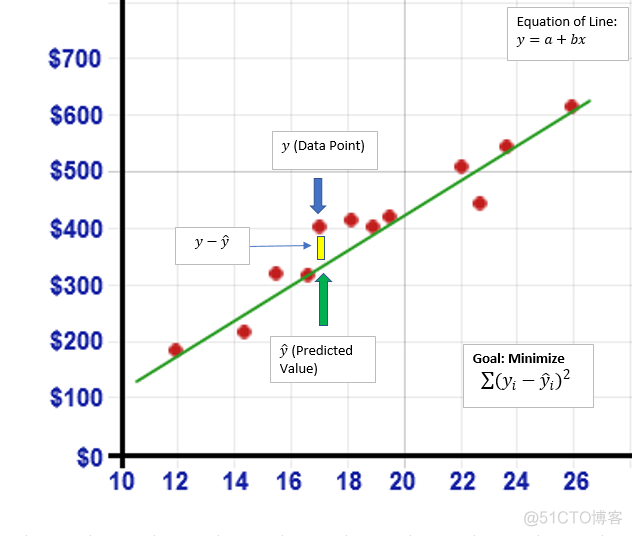
从本质上讲,这将构成我们对数据的最佳拟合。在OLS过程中通过数据集绘制了大量线条。该过程的目标是找到最佳拟合线,最小化平方误差和(SSE)与股票价格(y)的实际值以及我们在数据集中所有点的预测股票价格。这由下图表示。对于绘制的每条线,数据集中的每个点与模型输出的相应预测值之间存在差异。将这些差异中的每一个加起来并平方以产生平方和。从列表中,我们采用最小值导致我们的最佳匹配线。考虑下图:
from matplotlib import style
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import quandl
import datetime
style.use('ggplot')
#Dates
start_date = datetime.date(2017,1,3)
t_date=start_date, end_date=end_date, collapse="daily")
df = df.reset_index()
prices = np.reshape(prices, (len(prices), 1))', linewidth=3, label = 'Predicted Price') #plotting the line made by linear regression
plt.title('Linear Regression | Time vs. Price')
plt.legend()
predicted_price =regressor.predict(date)输出:
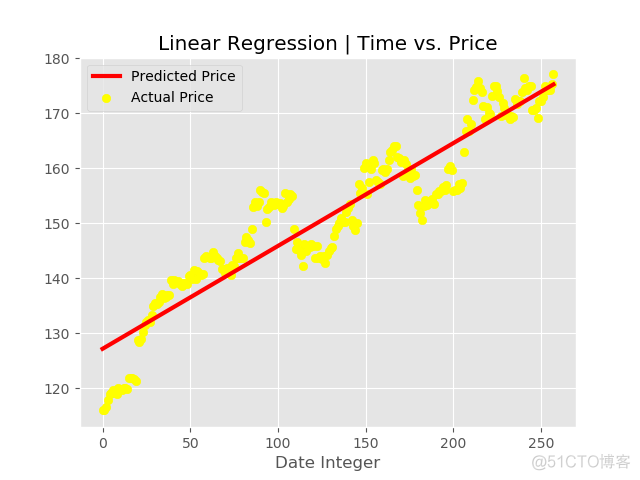
预测日期输入价格:
创建训练/测试集et
xtrain, x , ytrain)
#Train
plt.title('Linear Regression | Time vs. Price')
#Test Set Graph
plt.scatter(xtest, ytest, color='yellow', label= 'Actual Price') #plotting the initial datapoints
plt.plot(xtest, regressor.predict(xtest), color='blue', linewidth=3, label = 'Predicted Price') #plotting
plt.show()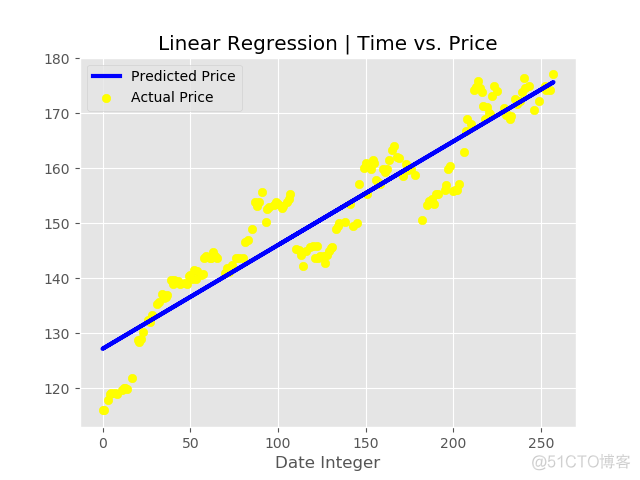
测试集:
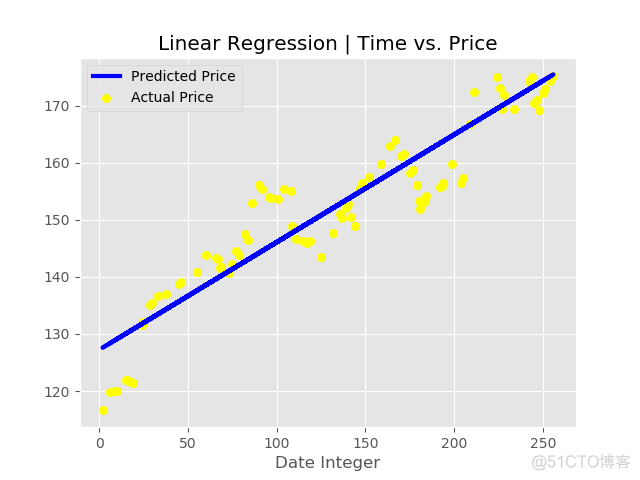
参考文献

1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用
8.R语言如何做马尔科夫转换模型markov switching model























