理一理基础优化理论,解释一下深度学习中的一阶梯度下降遇到的病态曲率(pathological curvature)问题。当海森矩阵condition number很大时,一阶梯度下降收敛很慢,无论是对鞍点还是局部极值点而言都不是个好事。
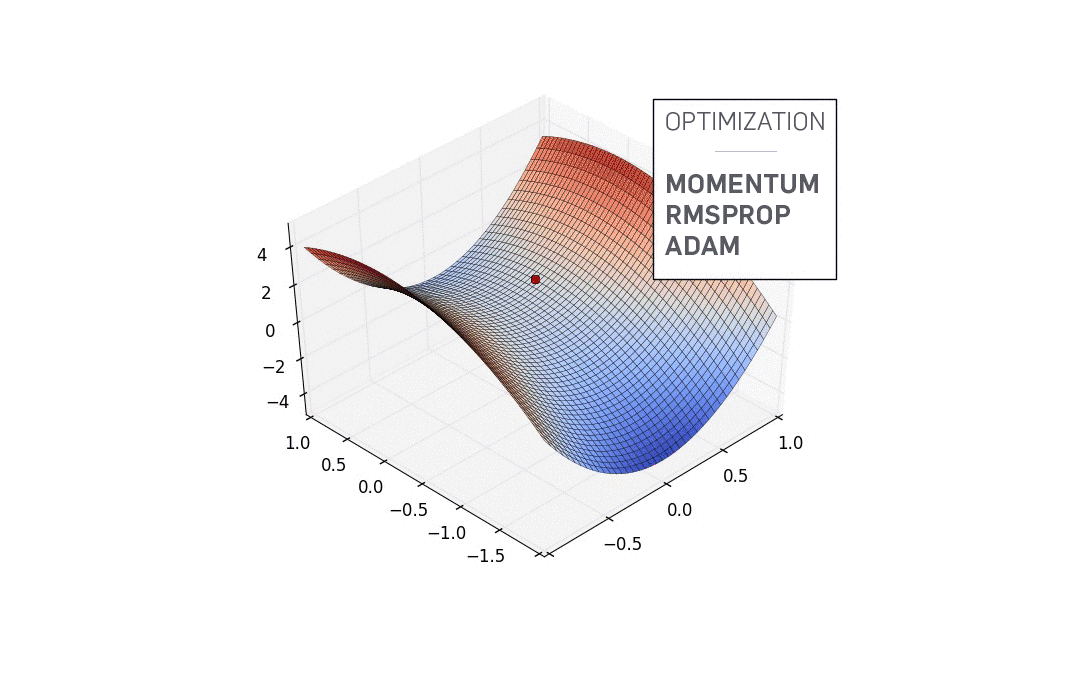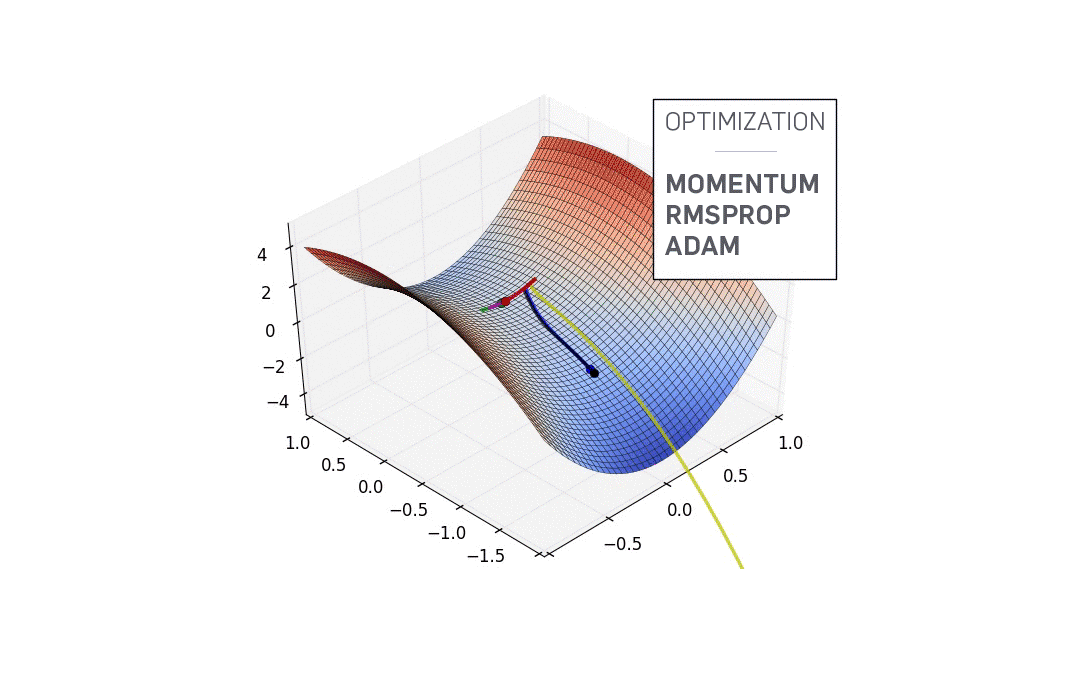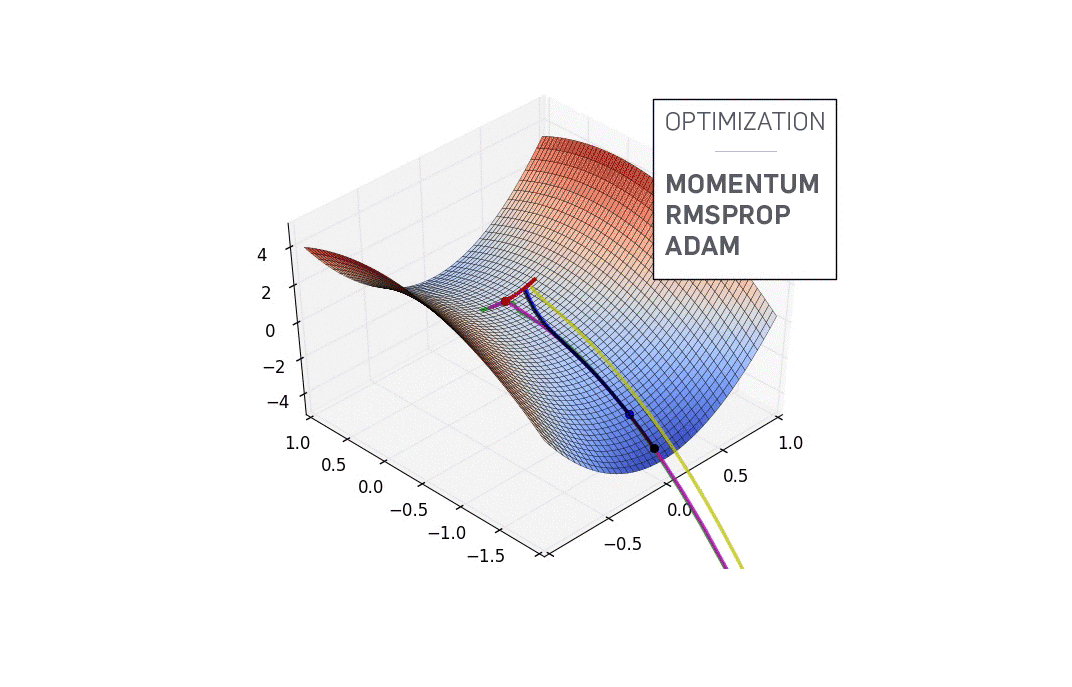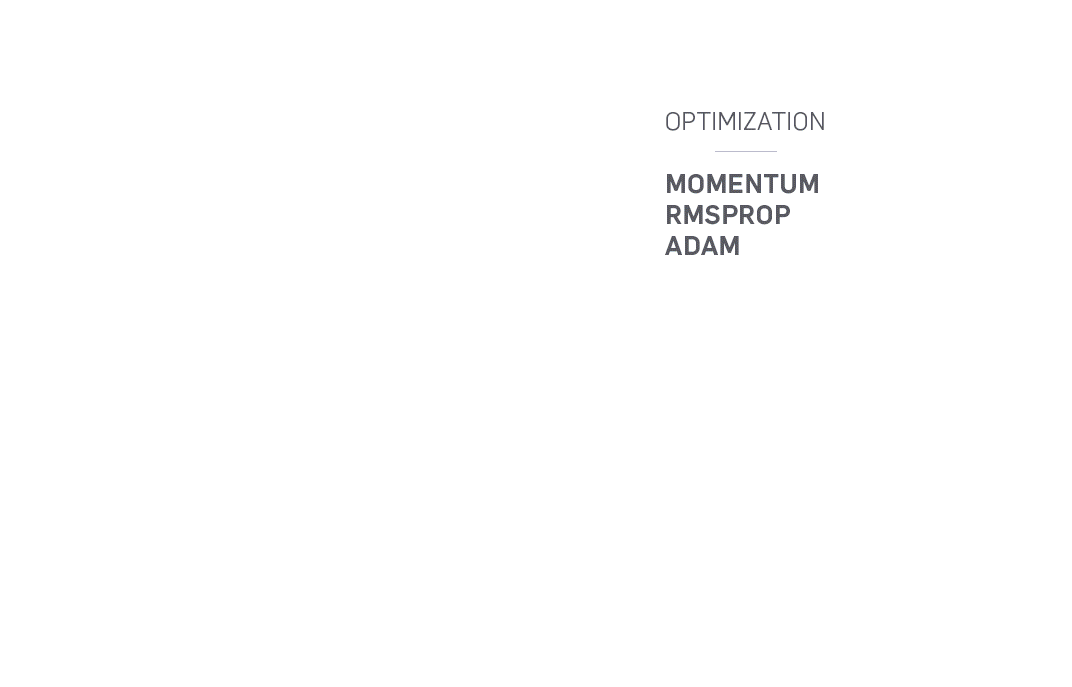
鞍点
$f'(x)=0$时函数不一定抵达局部最优解,还可能是鞍点(见上图),此时还必须根据二阶导数确定。
| $f'(x)$ | $f''(x)$ | $f(x)$ |
|---|---|---|
| $f'(x)=0$ | $f''(x)>0$ | 局部最小值 |
| $f'(x)=0$ | $f''(x)<0$ | 局部最大值 |
| $f'(x)=0$ | $f''(x)=0$ | 局部极值或鞍点 |
对角化
如果一个矩阵$A$可分解为如下乘积:
A=WΛW−1A=WΛW−1
其中,$W$为可逆矩阵,$\Sigma$是对角矩阵,则$A$是可对角化(diagonalizable)的。$W$的列向量$a_i$是$A$的特征向量,$\Sigma$的主对角线元素为特征向量对应的特征值。亦即:
WΛ=(a1a2…an)=⎡⎣⎢⎢⎢⎢⎢λ10⋮00λ2⋯⋯⋯⋯⋱000⋮λn⎤⎦⎥⎥⎥⎥⎥(1)W=(a1a2…an)(1)Λ=[λ10⋯00λ2⋯0⋮⋯⋱⋮0⋯0λn]
于是,
WΛ=(λ1a1λ2a2…λnan)WΛ=(λ1a1λ2a2…λnan)
$W$中的$n$个特征向量为标准正交基,即满足$W^TW=I$,等价于$W^T=W^{-1}$,也等价于$W$是Unitary Matrix。
由于对角化定义在方阵上,不适用于一般矩阵。一般矩阵的“对角化”就是大名鼎鼎的奇异值分解了。
奇异值分解
Am×n=Um×mΣm×nVTn×nAm×n=Um×mΣm×nVn×nT
其中,$AA^T$的特征向量stack为$U$,$A^TA$的特征向量stack为$V$,奇异值矩阵$\Sigma$中对角线元素为$\sigma_i = \frac{Av_i}{u_i} $。
Hessian 矩阵
一阶导数衡量梯度,二阶导数衡量曲率(curvature)。当 $f''(x)<0$, $f(x)$ 往上弯曲;当 $f''(x)>0$时,$f(x)$ 往下弯曲,一个单变量函数的二阶导数如下图所示。

对于多变量函数$f(x, y, z, \dots)$,它的偏导数就是Hessian矩阵:
Hf=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂2f∂x2∂2f∂y∂x∂2f∂z∂x⋮∂2f∂x∂y∂2f∂y2∂2f∂z∂y⋮∂2f∂x∂z∂2f∂y∂z∂2f∂z2⋮⋯⋯⋯⋱⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥Hf=[∂2f∂x2∂2f∂x∂y∂2f∂x∂z⋯∂2f∂y∂x∂2f∂y2∂2f∂y∂z⋯∂2f∂z∂x∂2f∂z∂y∂2f∂z2⋯⋮⋮⋮⋱]
$Hf$并不是一个普通的矩阵,而是一个由函数构成的矩阵。也就是说,$\textbf{H}f$的具体取值只有在给定变量值$(x_0, y_0, \dots)$时才能得到。
Hf(x0,y0,…)=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂2f∂x2(x0,y0,…)∂2f∂y∂x(x0,y0,…)⋮∂2f∂x∂y(x0,y0,…)∂2f∂y2(x0,y0,…)⋮⋯⋯⋱⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥Hf(x0,y0,…)=[∂2f∂x2(x0,y0,…)∂2f∂x∂y(x0,y0,…)⋯∂2f∂y∂x(x0,y0,…)∂2f∂y2(x0,y0,…)⋯⋮⋮⋱]
由于$Hf$是对称的实数矩阵:
δ2δxiδxjf(x)=δ2δxjδxif(x)⟹Hij=Hjiδ2δxiδxjf(x)=δ2δxjδxif(x)⟹Hij=Hji
所以它一定是可对角化的。对任意实数对称$n \times n$的矩阵$H$,有如下结论成立:
∀v∈Rn,||v||=1⟹vTHv≤λmax∀v∈Rn,||v||=1⟹vTHv≤λmax
证明如下:
由对角化形式$H = Q\Lambda Q^T$得到${\bf v}^TH{\bf v} = {\bf v}^TQ\Lambda Q^T{\bf v}$。定义一个由$\bf{v}$经过$Q^T$转换的向量${\bf y} = Q^T{\bf v}$,于是
vTHv=yTΛy(2)(2)vTHv=yTΛy
将对角矩阵$\Lambda$定义(1)代入有:
yTΛy=λmaxy21+λ2y22+⋯+λminy2N≤λmaxy21+λmaxy22+⋯+λmaxy2N=λmax(y21+y22+⋯y2N)=λmaxyTy⟹yTΛy≤λmaxyTy(3)yTΛy=λmaxy12+λ2y22+⋯+λminyN2≤λmaxy12+λmaxy22+⋯+λmaxyN2=λmax(y12+y22+⋯yN2)=λmaxyTy(3)⟹yTΛy≤λmaxyTy
由于$Q^{-1} = Q^T, QQ^T = I$,所以
yTy=vTQQTv=vTv(4)(4)yTy=vTQQTv=vTv
将式(4)代入式(3),有
yTΛy≤λmaxyTy(5)(5)yTΛy≤λmaxyTy
将式(2)代入式(5),有
vTHv≤λmaxvTvvTHv≤λmaxvTv
根据定义${\bf v}^T{\bf v} = \|{\bf v}\|^2$并且$\|{\bf v}\| = 1$,所以
vTHv≤λmax(6)(6)vTHv≤λmax
Condition Number of Hessian
任意可对角化矩阵的Condition Number定义如下:
maxi,j∣∣∣λiλj∣∣∣maxi,j|λiλj|
line search
在使用line search确定学习率的梯度下降中,参数点可看做首先往梯度最陡峭方向的垂线方向移动一个步长,接着往次陡峭方向移动一个步长。比如$2$个参数的损失函数:

将上面的等高线还原为3d的爬山问题,则如下图所示:

$3$个参数:


$N$个参数:

步长(学习率$\epsilon$)是通过如下方式估计的。
根据泰勒级数
f(x)=∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+f′′(a)2!(x−a)2+f′′′(a)3!(x−a)3+⋯f(x)=∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯
有
f(x)f(x)f(x(0)−ϵg)=f(x(0))+(x−x(0))Tg+12(x−x(0))TH(x−x(0))+…其中 g 为偏导数向量≈f(x(0))+(x−x(0))Tg+12(x−x(0))TH(x−x(0))≈f(x(0))−ϵgTg+12ϵ2gTHg 令x=x(0)−ϵg,ϵ∈(0,1)(7)f(x)=f(x(0))+(x−x(0))Tg+12(x−x(0))TH(x−x(0))+…其中 g 为偏导数向量f(x)≈f(x(0))+(x−x(0))Tg+12(x−x(0))TH(x−x(0))(7)f(x(0)−ϵg)≈f(x(0))−ϵgTg+12ϵ2gTHg 令x=x(0)−ϵg,ϵ∈(0,1)
这就是梯度下降$x\leftarrow x-\epsilon g$与海森矩阵的联系,$\epsilon$就是学习率。
当$g^T H g\le0$时,$\epsilon$增加会导致$f(x)$减小。但$\epsilon$不能太大,因为$\epsilon $越大泰勒级数中的$\approx$越不准。当$g^T H g>0$时,增大$\epsilon$不一定导致损失函数增加或减小。此时,对式(7)中的$\epsilon$求导,得到最佳学习率为:
ϵ∗=gTggTHg⩾gTggTgλmax=1λmax利用式(7) gTHg⩽gTgλmax.(8)(8)ϵ∗=gTggTHg⩾gTggTgλmax=1λmax利用式(7) gTHg⩽gTgλmax.
$\lambda_{\max}$是$H$的最大特征值。于是海森矩阵决定了最佳学习率的下界。在使用最佳学习率的情况下,将式(8)代入式(7)有
f(x(0)−ϵ∗g)≈f(x(0))−12ϵ∗gTgf(x(0)−ϵ∗g)≈f(x(0))−12ϵ∗gTg
如果海森矩阵的condition number很差(poor,很大)的话,损失函数在最陡峭的方向的梯度相较于其他方向非常小。如果此时恰好离最优值不远,则非常不幸。

梯度下降要么下降的很慢,要么步长太大跑得太远。

如同在一个狭长的峡谷中一样,梯度下降在两边的峭壁上反复碰撞,很少顺着峡谷往谷底走。

如果有种方法能让参数点在峭壁上采取较小步长,慢慢移动到谷底(而不是一下子撞到对面),然后快速顺流而下就好了。一阶梯度下降只考虑一阶梯度,不知道损失函数的曲率是如何变化的,也就是说不知道下一步会不会离开峭壁。解决方法之一是考虑了二阶梯度的牛顿法。
牛顿法
损失函数的泰勒展开近似,以及相应的导数近似为:
f(x)df(x)dΔx≈f(xn)+f′(xn)Δx+12f′′(xn)Δx2≈f′(xn)+f′′(xn)Δxf(x)≈f(xn)+f′(xn)Δx+12f″(xn)Δx2df(x)dΔx≈f′(xn)+f″(xn)Δx
令导数为零,找到极值点:
f′(xn)+f′′(xn)Δx=0Δx=−f′(xn)f′′(xn)f′(xn)+f″(xn)Δx=0Δx=−f′(xn)f″(xn)
执行一次迭代:
xn+1=xn+Δx=xn−f′(xn)f′′(xn)=xn−[Hf(xn)]−1f′(xn)xn+1=xn+Δx=xn−f′(xn)f″(xn)=xn−[Hf(xn)]−1f′(xn)
写成梯度下降的形式:
x′=x−[Hf(x)]−1f′(x)x′=x−[Hf(x)]−1f′(x)
其中,学习率
ϵ=[Hf(x)]−1f′(x)ϵ=[Hf(x)]−1f′(x)
学习率与曲率成反比,也就是说在曲率大的方向(垂直于峭壁)的学习率小,而在曲率小的方向(平行于峭壁)的学习率大。也就是是说此时的梯度下降在顺流而下的方向的学习率更大,也就更快收敛了。





















