14 最长公共前缀

01

题目信息

题目地址：

https://leetcode-cn.com/problems/longest-common-prefix/

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]

输出: "fl"

示例 2:

输入: ["dog","racecar","car"]

输出: ""

解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

 

02

解法一：横向比较

 

去找到多个串的公共前缀不知道，但我们至少知道找两个串的公共前缀。于是两两一组用上次公共串找下公共直到n-1次迭代完成最终公共前缀，那么像第一个示例三个串，就需要2次迭代

也就是说我们用一个公共前缀与下一个得到公共前缀然后更新覆盖，开始下一次迭代。那么一开始我们指定strs[0]为第一代的公共前缀，下面是初次提交成功的代码：

public String longestCommonPrefix(String[] strs){
    int n = strs.length;
    if(strs.length == 0) return "";
    //最初公共前缀
    String common = strs[0];
    //两两一次共n-1次迭代
    for(int i = 1; i < n; i++){
        //一次迭代的过程
        int j = 0;
        char[] cur = common.toCharArray();
        char[] next = strs[i].toCharArray();
        //strs数组与两个字符串边界
        if(next.length == 0) return "";
        while( j < cur.length && j < next.length ){
            // 扫描到不同了，那么这个索引在最后一个相同的后面一个
            if(cur[j] != next[j]){
                common = common.substring(0,j);//注意区间左闭右开
                break;
            // 没有扫描到不同但但已经结尾了，那么索引就是相同的最后一个
            }else if(j == cur.length - 1 || j == next.length - 1){
                common = common.substring(0,j+1);
                break;
            }
            j++;
        }
    }
    return common;
}

但这段代码是存在问题的，我们要考虑的问题是在循环里面的操作能不能减少，虽然时间复杂度不会变化。但减少循环体的操作也可以成倍的提升，观察代码首次迭代多少次就一个for循环没有什么问题，那么重点关注的是一次迭代这个过程的代码。我们这段代码拿出来：

while( j < cur.length && j < next.length ){
    // 扫描到不同了，那么这个索引在最后一个相同的后面一个
    if(cur[j] != next[j]){
        common = common.substring(0,j);//注意区间左闭右开
        break;
    // 没有扫描到不同但但已经结尾了，那么索引就是相同的最后一个
    }else if(j == cur.length - 1 || i == next.length - 1){
        common = common.substring(0,i+1);
        break;
    }
    j++;
}

 

先看循环体，因为两段if都有break，那么有三段只能走一个。我们想一想两段if的操作是不是可以合并的。聪明的小伙伴应该能很快反应过来，无非是有木有扫描超过导致是截取[ 0 , j )和[ 0 , j+1 )，那么其实只要不满足两个相等就出循环那么索引都是在最后相等后加了1，根本不用判断截取[ 0 , j )即可。代码立刻可以减少一部分

while( j < cur.length && j < next.length && cur[j] == next[j]){
    j++;
}
common = common.substring(0,j);//注意区间左闭右开

 

同时它也减少了我们在循环里的操作。如果循环是n次，那么里面有2-3次操作那么次数就是2-3n，尽量去减少里层循环的操作次数。除了循环体之外while条件也是随着循环被执行因为是​​短路与​​可能执行一个结束也可能执行三个式子，所以我们可以减少一次

int length = cur.length > next.length ? next.length : cur.length;
while( j < length && cur[j] == next[j]){
    j++;
}
common = common.substring(0,j);//注意区间左闭右开

 

这就相当于我们往外层添加了一次操作但减少了循环的一次操作，这些其实优化都不大但是在不换解题思维以及数据结构等等我们可以去考虑的优化点

public String longestCommonPrefix(String[] strs){
    int n = strs.length;
    if(strs.length == 0) return "";
    //最初公共前缀
    String common = strs[0];
    //两两一次共n-1次迭代
    for(int i = 1; i < n; i++){
        //一次迭代的过程
        int j = 0;
        char[] cur = common.toCharArray();
        char[] next = strs[i].toCharArray();
        //strs数组与两个字符串边界
        if(next.length == 0) return "";
        int length = cur.length > next.length ? next.length : cur.length;
        while( j < length && cur[j] == next[j]){
            j++;
        }
        common = common.substring(0,j);//注意区间左闭右开
    }
    return common;
}

 

 

03

解法二：纵向比较

 

其实最开始我想到的解法就是纵向比较同时扫描多个串每个串的字符都相等再同时往后扫描直到有第一个不同就终止。

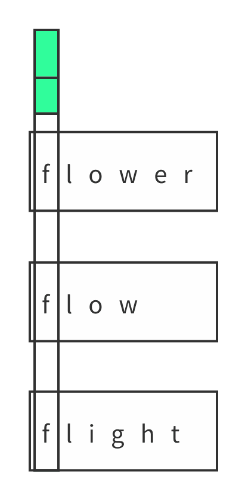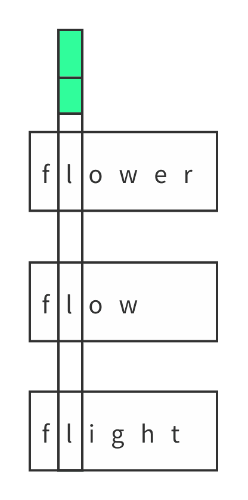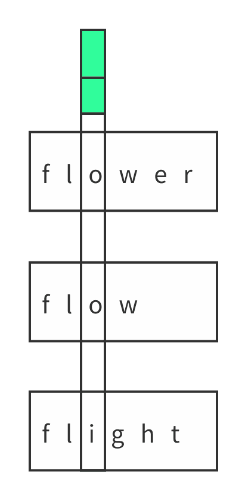
但当时只有一个直观的想法想着一字排开比较相等然后感觉处理不了就想到横向的比较好写

//伪代码
int i = 0;
while( i < min(length) && str1[i] == str2[i]==..... ){
    i++;
}

 

其实这里取一个字符串遍历，在一次遍历里面遍历数组的其他的字符串都进行比较即可

public String longestCommonPrefix(String[] strs) {
    //为空返回""
    if (strs.length == 0) return "";
    //取数组减少charAt在循环体
    char[] p = str[0].toCharArray();
    int n = p.length;
    for (int i = 0; i < n; i++) {
        char c = p[i];
        //依次判断直到不等出现，截取返回
        for (int j = 1; j < strs.length; j++) {
            if (i == strs[j].length() || strs[j].charAt(i) != c) {
                return strs[0].substring(0, i);
            }
        }
    }
    return strs[0];
}

 

04

解法三：变体（解一）

 

我们出了通过循环扫描比较得到两串的公共前缀，还可以通过前缀是否包含可以用a.startsWith(b)判断是否以起始索引包含另一个串，或者用a.indexOf(b) == 0 来判断，没有则删减一位直到找到公共前缀开始下个迭代和解一是一样的只是找公共前缀的方式不同

public String longestCommonPrefix(String[] strs) {
    //为空返回""
    if (strs.length == 0) return "";
    String common = strs[0];
    for (String str : strs) {
        // 若common已经减为""，则说明无公共前缀，直接返回
        if (common == "") return common;
        // 若common在当前str中匹配不上，则减少字符串common的长度，再次尝试匹配
        while (!str.startsWith(common)) {
            common = common.substring(0,common.length() - 1);
        }
    }
    return common;
}

 

05

总结

 

总体而言的话其实时间复杂度都是比较高的，毕竟都使用了substring等方法超过n的三次方都差不多所以没有较优解。也是和上一题差不多两题都是体会迭代的一个过程因此也都可以转成递归的形式，那就还可以分治分到最后都是两两一组然后求解自底向上之后会介绍，到此LeetCode初级算法合集中的字符串系列全部完成，开启下个篇章链表。