Python roc曲线的置信区间

转载

goody 2024-10-31 20:35:07

文章标签 Python roc曲线的置信区间正例召回率样本分布 文章分类 Python 后端开发

1.ROC曲线简介

2. AUC（ROC曲线的线下面积）

3.ROC曲线的优点

4. ROC曲线和PR曲线的区别：

5. ROC曲线的绘制

1.ROC曲线简介

ROC曲线从图标上看，是以TPR为纵轴，FPR为横轴的图标：

要绘制ROC曲线，除了要计算TPR和FPR，还要不断调整置信度阈值，来得到不同的分类数据，从而得到多组TPR和FPR来绘制ROC曲线。

为什么要调整置信度阈值？因为不同的阈值，网络的输出结果数量会不一样，阈值低，输出结果就多，阈值高，输出结果就少。

然后再通过输出结果来计算TPR和FPR。

Python roc曲线的置信区间_正例

TPR(True Position Rate，真阳率)：即一堆数据中，正样本被网络成功识别出它是正样本的比例

Python roc曲线的置信区间_召回率_02

TP：(True Postion，真阳样本)：即本来是正样本，被网络识别为正的样本

P：所有的正样本

FPR(False Position Rate，假阳率)：即一堆数据中，负样本被网络误识别成正样本的比例

Python roc曲线的置信区间_正例_03

FP：(False Postion，假阳样本)：即本来是负样本，但被网络识别为正的样本

N：所有的负样本

可以看出，当一个样本被分类器判为正例，若其本身是正例，则TPR增加；若其本身是负例，则FPR增加。

可以看到曲线越靠左上角，网络性能越好。因为越靠左上角，TPR越大，代表正样本被正确识别的比例越高，同时FPR也越小，代表负样本被误识别成正样本的比例越小。例越小。细心的朋友可以发现，上图的ROC曲线中，有一条对角虚线，这表示TPR=FPR的随机线，意思是这时候所有样本（无论是正样本还是负样本）都会被网络识别出正样本，这就表示这时候的网络是没有识别能力的。

2. AUC（ROC曲线的线下面积）

ROC曲线是一个图标曲线，但要量化地评估模型，即用一个数值来评价模型，还要用AUC，AUC是ROC的线下面积:

一般来说，AUC越高越好。

AUC物理意义：

先说结论：网络的分类结果按置信度从高到低排序，其中肯定有正样本的也有负样本的，AUC越高，代表排在负样本前的正样本就越多，换句话说，就是在正样本中置信度比负样本置信度高的正样本个数就越多。下面举个例子证明：

现在假设有一个训练好的二分类器对10个正负样本（正例5个，负例5个）预测，得分按高到低排序得到的最好预测结果为[1, 1, 1, 1, 1, 0, 0, 0, 0, 0]，即5个正例均排在5个负例前面，正例排在负例前面的概率为100%。然后绘制其ROC曲线，由于是10个样本，除开原点我们需要描10个点，如下：

可以看到ROC曲线为高度是1的横线。AUC=1，为完美分类器，表示正例排在负例前面的概率的确为100%

Python roc曲线的置信区间_样本分布_04

但当网络的预测排序结果为：[1, 1, 1, 1, 0, 1, 0, 0, 0, 0]。ROC曲线就变成了：

Python roc曲线的置信区间_样本分布_05

自然AUC也变小了。

在看如果网络的预测排序结果为：[1, 1, 1, 0, 1, 0, 1, 0, 0, 0]，ROC的曲线就又变成了：

Python roc曲线的置信区间_样本分布_06

AUC也进一步变小了。所以AUC的意义就是，网络的预测结果排序后，真正样本能排在真负样本前面的概率，换句话说就是，真正样本置信度能比真负样本置信度高的概率。

而阴影面积就是，真负样本置信度比真正样本置信度高的概率。

AUC值对模型性能的判断标准：

AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

不同模型之间选择最优模型：

不同的模型对应的ROC曲线中，AUC值大的模型性能自然相对较好。而当AUC值近似相等时，有两种情况：第一种是ROC曲线之间没有交点；第二种是ROC曲线之间存在交点。在两个模型AUC值相等时，并不代表两个模型的分类性能也相等。

ROC曲线之间没有交点

如下图所示，A，B，C三个模型对应的ROC曲线之间交点，且AUC值是不相等的，此时明显更靠近(0,1)(0,1)(0,1)点的A模型的分类性能会更好。

敏感度：即TPR，代表了正样本被分对的比例，衡量了网络对正样本的识别能力(数值上等于召回率)

举例若现在的目的是要识别出病人，则病人是正样本，正常人是负样本。

敏感度越高，模型识别出的病人就越多，漏诊的几率就越小。

特异度：即1-FPR，代表了将负样本识别为负样本的情况占所有负样本的比例，衡量了分类器对负样本的识别能力。

特异度越高，则模型识别出的正常人就越多，误判的几率就越小。

Python roc曲线的置信区间_正例_07

ROC曲线之间存在交点

如下图所示，模型A、B对应的ROC曲线相交却AUC值相等，此时就需要具体问题具体分析：当需要高Sensitivity值(敏感度，TPR)时，A模型好过B；当需要高Specificity值(特异度，1-FPR)时，B模型好过A。

Python roc曲线的置信区间_样本分布_08

3.ROC曲线的优点

ROC曲线和AUC这个评价标准最大的优势所是：

其他的评价标准如准确率、召回率都会受到测试集样本分布的影响，即对于同一模型，采用这些指标进行性能评估的话，如果输入的样本中正负样本分布发生变化，则最终的这些评价标准的数值也会变化，这种最终结果会被输入样本分布影响的特性，显然使得这些指标在评估某个样本性能时会对输入样本产生依赖，不能很客观的反应模型的性能。

而ROC则很小受输入样本比例影响，即就算负样本增大10倍，ROC曲线也是几乎不变的，而其他如PR曲线就会变化剧烈。

下面来解释这个原因：

下图是一个混淆矩阵。我们已知ROC的横轴和纵轴分别是FPR和TPR。从(b)看出，TPR只受TP和FN影响，从混淆矩阵看出，TP和FN都属于正样本，所以增加负样本，对TPR是没影响的。而FPR只受FP和TN影响，从混淆矩阵看出，FP和TN都是负样本，所以增加10倍负样本的话，FP和FP+TN也是按比例增加的，所以实际来说，几乎没变化。因此ROC曲线变化不大。

Python roc曲线的置信区间_Python roc曲线的置信区间_09

接下来我们看看PR曲线，PR曲线横轴是召唤率(Recall)，纵轴是准确率(Precision)，若增大10倍负样本，TP和FN都不变，因为都属于正样本，所以召回率Recall是不变的。但是Precision呢，负样本增加，FP也会增加，所以Precision是会变的。所以PR曲线会受到正负样本比例的影响。

详细地我们来看一下下面这张图：

Python roc曲线的置信区间_召回率_10

(a)和(b)为在初始测试集上的ROC曲线和PR曲线，(c)和(d)为增加10倍负样本后的ROC曲线和PR曲线，可以看到ROC曲线并没怎么变化，但是PR曲线则变化剧烈。

4. ROC曲线和PR曲线的区别：

1. PR更关注正样本的分类情况，因为准确率和召回率都是算预测出正样本的比例。而ROC则兼顾正样本和负样本的分类情况。

2. 在测试样本的正负分布发生变化时，ROC基本不变，PR则会改变。当正负样本比例失调时，比如正样本1个，负样本100个，则ROC曲线变化不大，此时用PR曲线更加能反映出分类器性能的好坏。则ROC则能撇除正负样本分布的影响，来判断模型的能力。

5. ROC曲线的绘制

ROC计算过程如下：
1)首先每个样本都需要有一个label值，并且还需要一个预测的score值（即置信度，取值0到1）;
2)然后按这个score对样本由大到小进行排序，假设这些数据位于表格中的一列，从上到下依次降序;
3)现在从上到下按照样本点的取值进行划分，位于分界点上面的我们把它归为预测为正样本，位于分界点下面的归为负样本;
4)分别计算出此时的TPR和FPR，然后在图中绘制（FPR, TPR）点。

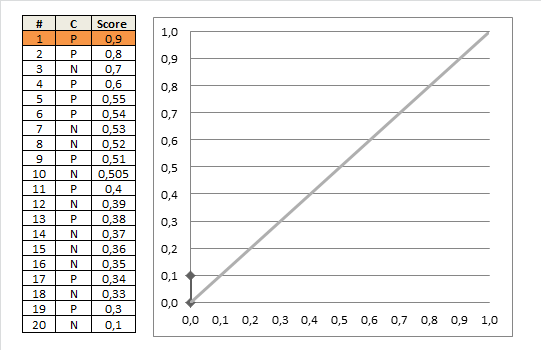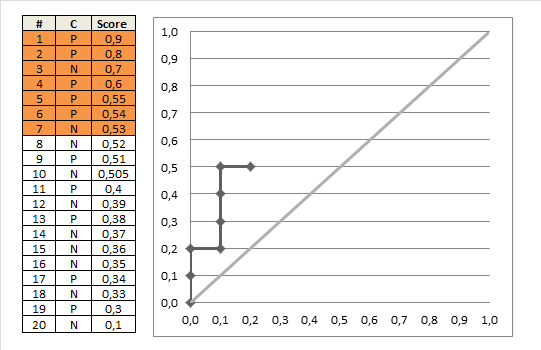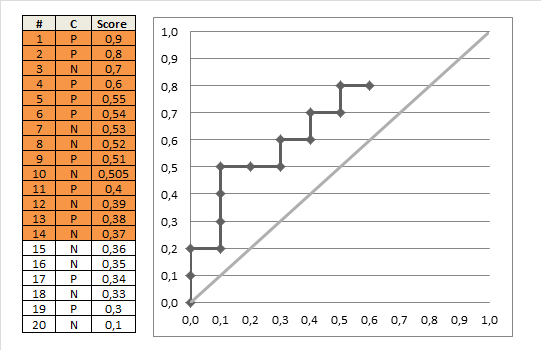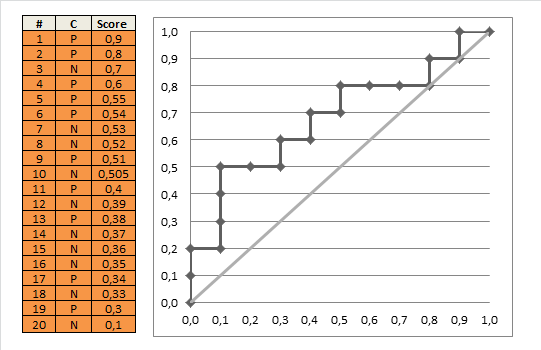
Python roc曲线的置信区间_召回率_11